Chapter 1: Introduction to the Howitzer Cart Experiment

The Howitzer cart is a fascinating physics demonstration. In this setup, a cart moves at a steady speed along a flat track. At a certain moment, a ball is projected straight upwards, only to fall back into the cart. Let's dive into the mechanics behind this intriguing phenomenon.

Section 1.1: Understanding the Motion of the Cart

To comprehend why the ball lands back in the cart, we begin with the motion equation for the cart. Since it travels on a horizontal path at a consistent velocity, we can express its position using the following kinematic formula:

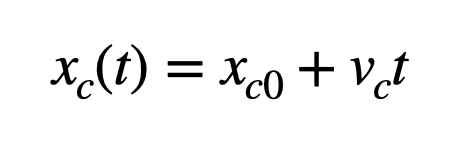
Here, ( x_c ) represents the position over time, ( x_{c0} ) is the initial position when ( t = 0 ), and ( v_c ) is the cart's velocity. When the ball is launched vertically (relative to the cart), it shares the same horizontal speed as the cart. During its flight, the only force acting on the ball is gravity, which does not affect its horizontal motion.

The projectile motion of the ball is described by the following kinematic equations:

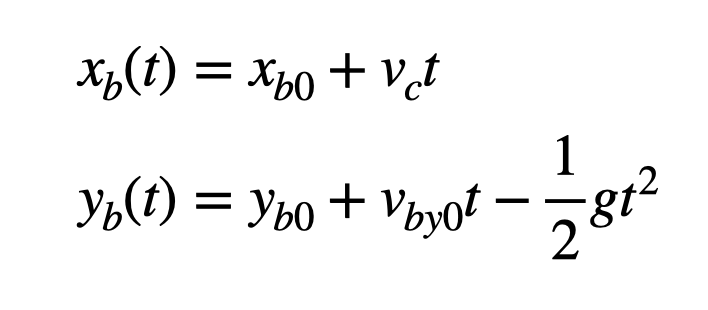
An essential takeaway is that if the ball's initial horizontal position coincides with that of the cart, it will always land back in the cart, making this demonstration particularly entertaining.

Now, let’s conduct a video analysis to extract data from this experiment. I will utilize Tracker Video Analysis, my preferred tool for such tasks.

A few quick notes: I placed a broken meter stick beside the track to help establish the distance scale in the video. Additionally, my camera was slightly tilted, but I can adjust the x-axis of the coordinate system to align with the track.

For the cart's position as a function of time, we observe:

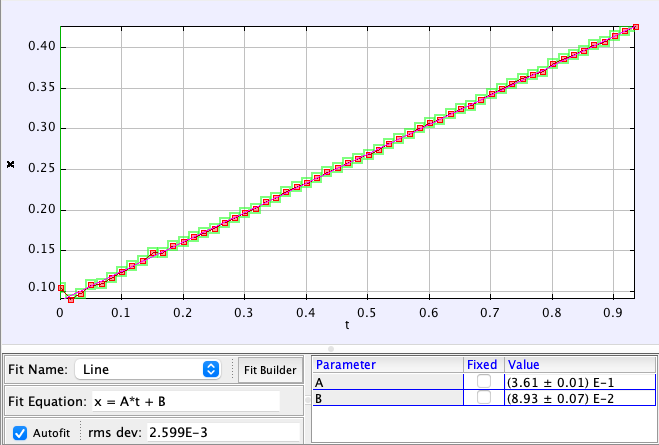
This confirms a constant velocity, as anticipated. The slope of the linear fit indicates that the cart travels at a speed of 0.361 meters per second.

Now, let’s examine the horizontal motion of the ball after it has been launched.

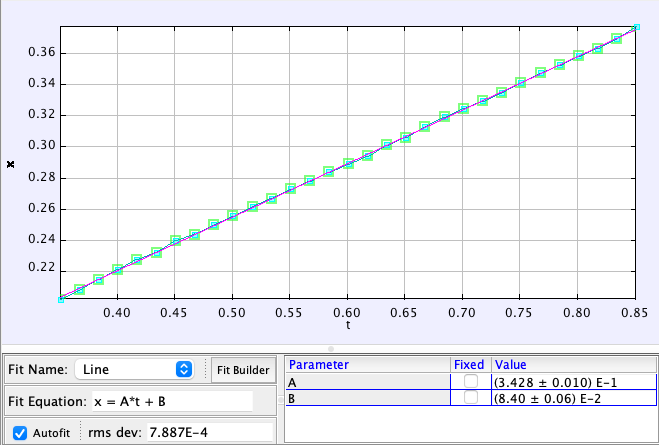
This graph also reveals a constant horizontal speed, closely matching that of the cart at 0.343 m/s. The slight discrepancy might stem from adjustments on the launcher, suggesting the ball may not have been launched perfectly vertically.

Next, we turn our attention to the vertical motion of the ball.

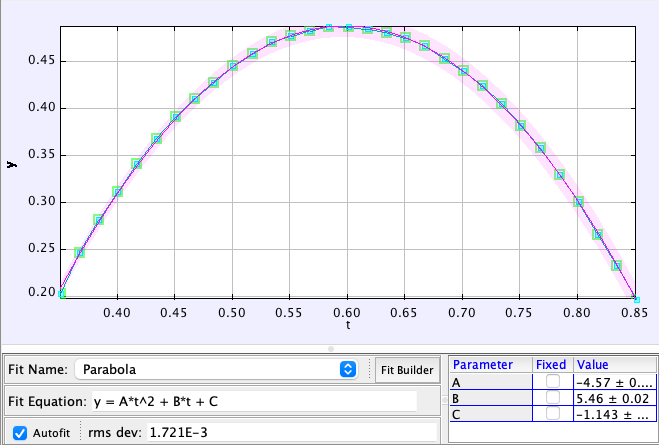
Given the constant acceleration due to gravity, the vertical position of the ball over time should exhibit a parabolic shape, which it does. The curve fit provides an acceleration of 9.14 m/s², slightly lower than the expected 9.8 m/s², likely due to the scaling error.

An interesting observation is the initial vertical velocity. The curve fit indicates a velocity of 5.46 m/s at ( t = 0 ) seconds, but since the ball was launched at 0.35 seconds, its actual velocity at launch was 2.03 m/s.

This suggests that the ball was not launched straight up; it had both horizontal and vertical components of velocity. However, since its horizontal speed matched that of the cart, it appeared to travel vertically from the cart's frame of reference.

Now, let’s consider a variation of this experiment.

Chapter 2: Howitzer Cart on an Incline

What happens if we repeat the demo, but this time the cart rolls down an incline? Will the ball still land in the cart, or will it overshoot or fall short? Let's find out.

Notice that the ball is still projected vertically with respect to the cart's motion. However, this time the cart accelerates rather than maintaining a constant speed.

To analyze this, let’s create a force diagram.

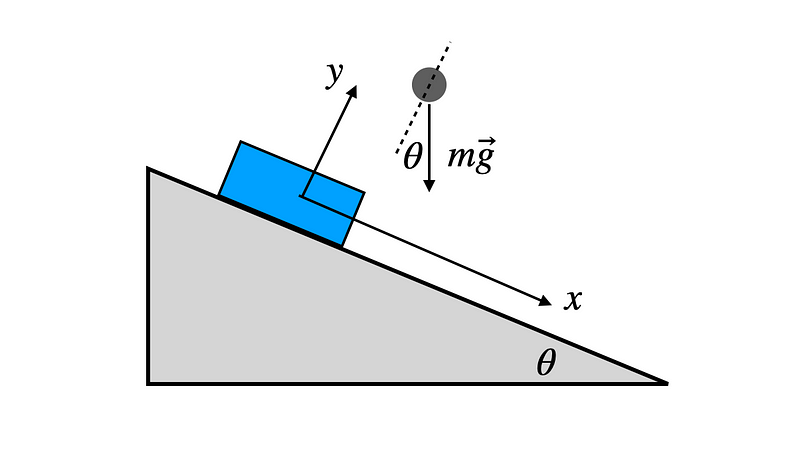
By orienting the x-axis along the incline, we can see there’s a component of gravitational force acting in the direction of the cart's motion. This leads us to the following motion equation for the cart.

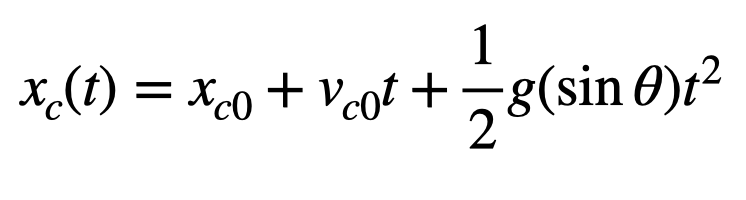
If we revert the incline angle to horizontal, the equation simplifies back to our earlier formula, as ( sin(theta) = 0 ).

Now, regarding the ball, the only force acting on it remains the gravitational force. However, it now experiences an x-component of that force, mirroring the horizontal force acting on the cart. This results in the following equations for the ball's motion.

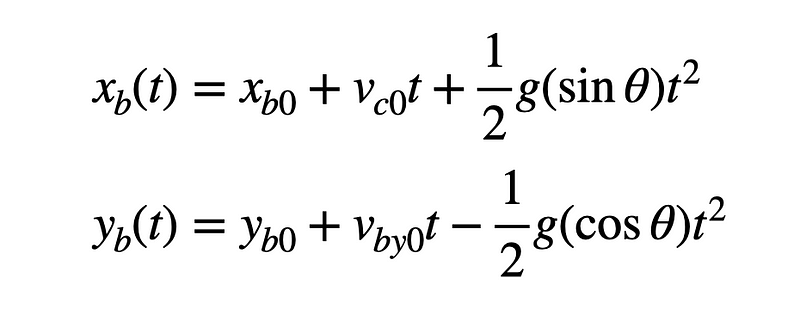
The critical point to note is that the motion equations for both the cart and the ball are identical in the x-direction, provided they start from the same position and have the same initial horizontal speed. This is why the ball continues to land back in the cart.

However, there’s an additional detail to consider: In this reference frame, where we’ve tilted the x-axis, the ball does not conform to the traditional "projectile motion" scenario since it accelerates in both the x and y directions.

Homework Assignments

Here are a few thought-provoking exercises to explore further:

1. Consider launching the ball straight up with respect to the cart's motion. What modifications could prevent the ball from landing back in the cart?
2. In the previous scenario, what adjustments could ensure the ball once again lands in the cart?
3. If the ball is launched at an angle relative to the cart, how might you measure the change in the cart's velocity? (Hint: consider momentum.)
4. Create a Python simulation of a Howitzer cart for a fun programming exercise.
5. Upon closely reviewing the video, you might notice that the ball appears smeared out. Why might this occur, and could this phenomenon be utilized to determine the ball's velocity in each frame?

Now, let's watch some videos that illustrate these concepts in action!

The first video titled "Kinematics Demo: Cart and Ball" offers a visual representation of the cart's motion and the projectile launched from it.

The second video, "Howitzer Cart: Inertial Reference Frames (Newton's 1st Law)," further explains how the laws of motion apply in this context.