# Understanding the Erdős-Szekeres Theorem: A Comprehensive Guide
Written on
Introduction to Monotonicity
In this article, we delve into a fascinating theorem proposed by mathematicians Paul Erdős (1913–1996) and George Szekeres (1911–2005) in 1935, which pertains to finite sequences of real numbers. The theorem is rooted in Ramsey Theory, which examines the circumstances under which order emerges from chaos.
The problem can be framed as a simple game: we sequentially list distinct numbers—ensuring no repetitions. The objective is to continue this process without forming a "long" monotone subsequence. Specifically, after writing down N numbers, an opponent can remove some, and the remaining numbers must not constitute a lengthy monotonic sequence (either entirely increasing or entirely decreasing). The definition of "long" will be clarified shortly. If we can prevent such a subsequence from appearing, we claim victory; otherwise, our opponent wins.
It is a well-established fact that:
Every infinite series of distinct real numbers contains either a monotonically increasing or a monotonically decreasing infinite subsequence.
The Erdős-Szekeres theorem presents a similar assertion for finite sequences:
Theorem [Erdős-Szekeres 1935]
For any given positive integers s and r, any sequence of distinct real numbers with a length of at least N = s*r + 1 will contain either a monotonically increasing subsequence of length s + 1 or a monotonically decreasing subsequence of length r + 1 (or both).

To clarify further, let’s set s = r = n, where n is a positive integer. If we list N = n² + 1 distinct real numbers, regardless of our selections, there will invariably be a monotonic subsequence of length n + 1. For instance, if we choose 10 numbers, at least one monotonic subsequence of length 4 is guaranteed. Consider this example of 10 numbers:
1, 10, 5, 6, 0, 2, 3, 11, 7, 4.
In the context of our game, if we define "long" as 4, our opponent can indeed win with the sequence above by selecting 1, 5, 6, and 11 (or other combinations). However, if we set "long" to 5, victory is ours, as no monotone subsequence of that length exists—demonstrating that the parameters outlined in the theorem are optimal.
A Beautiful Proof of the Erdős-Szekeres Theorem by Seidenberg (1959)
Numerous proofs exist for the Erdős-Szekeres theorem, but we will focus on one of the most elegant, likely worthy of being included in a notable mathematics anthology. For more insights into such literature, refer to the introduction of this article or the corresponding Wikipedia entry.
Now, let's proceed with our exploration, closely adhering to the presentation from the esteemed book “Extremal Combinatorics with Applications in Computer Science” by Stasys Jukna.
Let us denote a sequence of N distinct real numbers, where N = s*r + 1 for positive integers s and r. The first critical concept is that we assign two coordinates to each number in the sequence (considered as points in a plane):
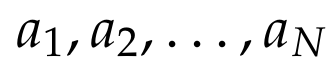
It’s important to note that in our definitions of x_i and y_i, we specifically require subsequences that include the term a_i. A significant observation is that:
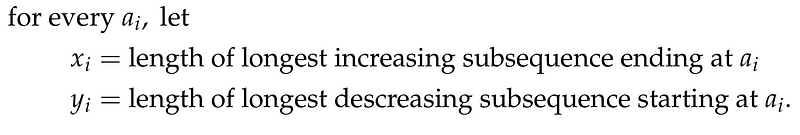
This indicates that for any two elements in the sequence, the corresponding points based on the defined coordinates will differ. For instance, if i < j, we can analyze two cases:
- If a_i < a_j: The longest increasing subsequence that concludes with a_i can be extended by a_j, thus x_i ≤ x_j + 1.
- If a_i > a_j: The longest decreasing subsequence that starts with a_i can be extended by a_j, leading to y_i ≤ y_j + 1.
This confirms our observation, relying crucially on the fact that all numbers in the sequence are distinct.
Now, we introduce the second pivotal idea of our proof—the celebrated pigeonhole principle! We construct an N x N grid.
As illustrated, we place each number a_i on the grid according to its coordinates (x_i, y_i). Here, the vertical axis represents the x-coordinate, while the horizontal axis corresponds to the y-coordinate.
Clearly, 1 ≤ x_i ≤ N and 1 ≤ y_i ≤ N for all i, ensuring every number occupies a grid cell. Furthermore, given our previous observation, no two numbers will occupy the same cell.
Since N > s*r, we have more numbers than the (s*r) shaded grid cells. If all numbers were to fall within the shaded region, the pigeonhole principle would necessitate that at least two numbers a_i and a_j share identical coordinates. Since this is not the case, we conclude that at least one number a_i must be located outside the shaded area. This implies either its x-coordinate exceeds s, its y-coordinate exceeds r, or both. Referring back to the definition of the (x,y)-coordinates, we derive the theorem's statement. This completes our proof!
To deepen your understanding, watch the video titled "CO5 The Erdős-Szekeres Theorem" for a detailed exploration of this topic.
Additionally, check out "A Maths Proof I Wished I Knew Earlier!! Erdős-Szekeres Theorem Using Pigeonhole Principle" for an engaging perspective on this theorem and its implications.