Understanding Linear Discriminant Analysis: A Comprehensive Guide
Written on
Chapter 1: Introduction to Linear Discriminant Analysis
This article serves as an introductory guide to Linear Discriminant Analysis (LDA), covering both its theoretical aspects and Python implementation.
Linear Discriminant Analysis (LDA) is a statistical method used to classify data points into distinct classes. It assumes that the data follows a Gaussian distribution.
Section 1.1: Overview of the Series
This post is part of a broader series focused on machine learning concepts. For a more extensive exploration, feel free to visit my personal blog linked here. Below is a brief outline of the series:
- Introduction to Machine Learning
- Understanding machine learning
- Selecting models in machine learning
- The curse of dimensionality
- Exploring Bayesian inference
- Regression
- Mechanics of linear regression
- Enhancing linear regression with basis functions and regularization
- Classification
- Introduction to classifiers
- Quadratic Discriminant Analysis (QDA)
- Linear Discriminant Analysis (LDA)
- Gaussian Naive Bayes
- Multiclass Logistic Regression using Gradient Descent
Section 1.2: Setup and Objectives
In the previous discussion, we explored Quadratic Discriminant Analysis (QDA). Much of the underlying theory for LDA aligns closely with that of QDA, which we will delve into now.
The primary distinction between LDA and QDA is that LDA operates with a single shared covariance matrix across classes, whereas QDA utilizes class-specific covariance matrices. It is crucial to understand that LDA is categorized under Gaussian Discriminant Analysis (GDA) models, which are generative in nature.
Given a training dataset of N input variables ( x ) alongside corresponding target variables ( t ), LDA posits that the class-conditional densities are normally distributed.
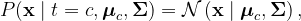
Where ( mu ) represents the class-specific mean vector and ( Sigma ) denotes the shared covariance matrix. By employing Bayes’ theorem, we can compute the posterior probability for each class.
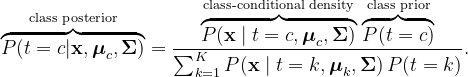
We can then classify ( x ) into its respective class.
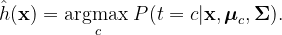
Section 1.3: Derivation and Training
The log-likelihood derivation for LDA follows a similar approach as that of QDA. The log-likelihood expression can be derived as follows:
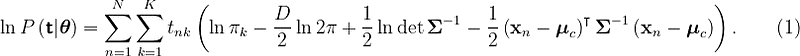
Examining the log-likelihood, we notice that the priors and means for each class remain unchanged between LDA and QDA, as derived in our previous post.
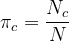
However, the shared covariance matrix differs significantly. By taking the derivative of the covariance matrix expression and setting it to zero, we arrive at:
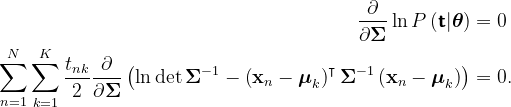
Utilizing matrix calculus, we can evaluate the derivative, which you can find detailed in my extended blog post.
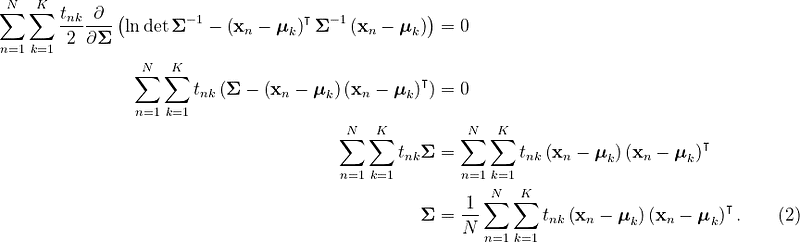
Ultimately, we discover that the shared covariance matrix is the covariance of all input variables combined. Thus, we classify using the following equation:
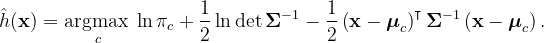
Chapter 2: Python Implementation of LDA
The following code snippet illustrates a straightforward implementation of LDA based on our discussion.
The first video, "StatQuest: Linear Discriminant Analysis (LDA) clearly explained," provides a clear overview of LDA concepts.
Additionally, we can visualize the data points, color-coded according to their respective classes, alongside the class distributions identified by our LDA model and the decision boundaries resulting from these distributions.
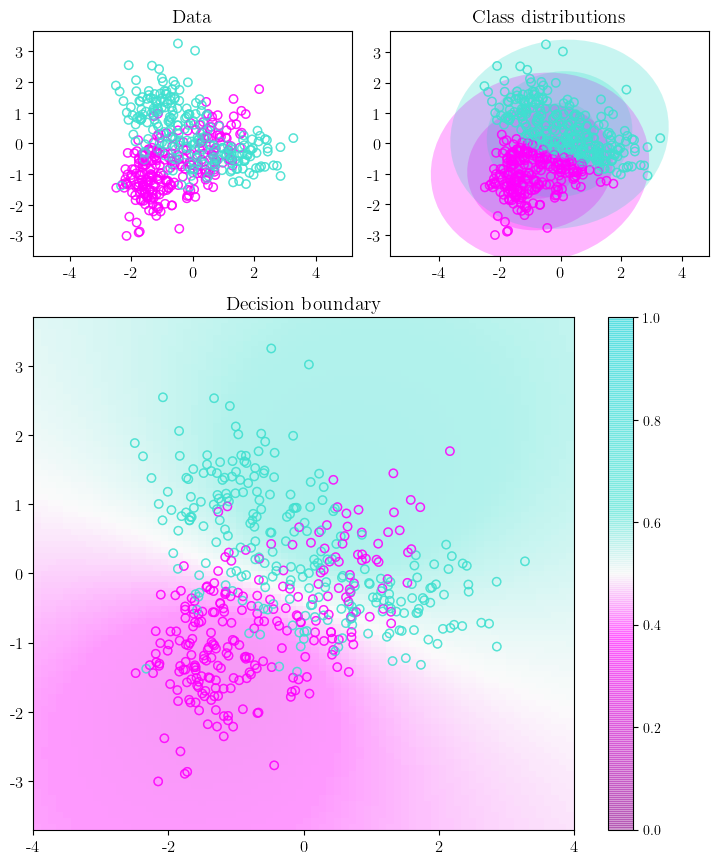
As observed, LDA enforces more restrictive decision boundaries due to its assumption that all classes share the same covariance matrix.
Section 2.1: Summary of Findings
To summarize, Linear Discriminant Analysis (LDA) is categorized as a generative model. It assumes that each class follows a Gaussian distribution. The key distinction between QDA and LDA lies in LDA's use of a shared covariance matrix across classes rather than class-specific covariance matrices. The shared covariance matrix, in essence, is the covariance of all input variables combined.
The second video, "Linear discriminant analysis explained | LDA algorithm in python," further elaborates on implementing LDA in Python.