A New Approach to Prime Number Detection with Python
Written on
Chapter 1: Introduction to Prime Detection
In this article, we aim to formulate a new method for calculating the divisors of a number, utilizing Python to verify our computations. This exploration serves as a candid experiment, inviting readers to witness my thought process and coding attempts as I tackle these calculations. Consequently, the writing style may appear unrefined, presenting my immediate thoughts and initial concepts rather than a polished narrative.
Section 1.1: Understanding Divisibility
To develop a function ( d ) that takes two positive integers ( k ) and ( n ) as inputs—returning 1 if ( k ) divides ( n ) and 0 otherwise—we can consider a couple of approaches. One straightforward method involves dividing ( n ) by ( k ) to check if the result is a whole number. Alternatively, we could multiply ( k ) by integers from 1 up to ( n ) and see if we hit ( n ).
For instance, let’s examine ( k = 3 ) and ( n = 6 ):
- ( 1 times 3 = 3 )
- ( 2 times 3 = 6 )
- ( 3 times 3 = 9 )
We achieve ( n ) on the second multiplication! It's important to note that there can only be one integer ( m ) for which ( k times m = n ). Our objective is to return 1 if such an ( m ) exists and 0 otherwise. Fortunately, there’s a neat mathematical approach to accomplish this.
Recall the property of complex exponentials: for any integer ( k ) and a suitable range, we can use this property to sum relevant integers and utilize integrals effectively.
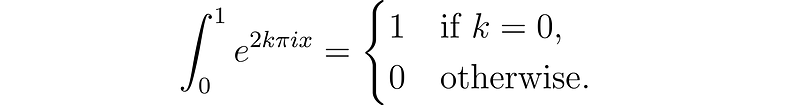
To formalize this, we can define the function ( d ) such that it adds 1 whenever ( n = k times m ). This means we could express this in a more comprehensive form, preferably by summing to infinity, leading to a more manageable fraction when dealing with geometric series.
However, interchanging the sum and integral requires careful consideration of absolute convergence. For geometric series to converge, the base must remain between -1 and 1. As the complex exponential maintains a modulus of 1, direct substitution with infinity is not feasible.
Section 1.2: Introducing a Damping Factor
To overcome this challenge, we will adjust our definition of ( d ) by introducing a damping factor that ensures convergence. Additionally, we'll sum from ( m = 0 ), assuming ( n ) is a natural number. We can express ( d ) as follows:
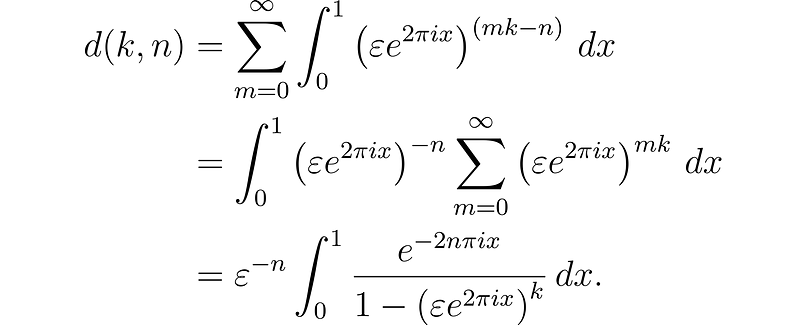
This adjustment does not alter the value of the integral. At this juncture, it is prudent to validate our findings using Python. Instead of applying the formula directly, we can compute the real part of the integrand to work with a tangible function.
We could visualize this through a plot, examining how ( d ) behaves at the divisors of 6.
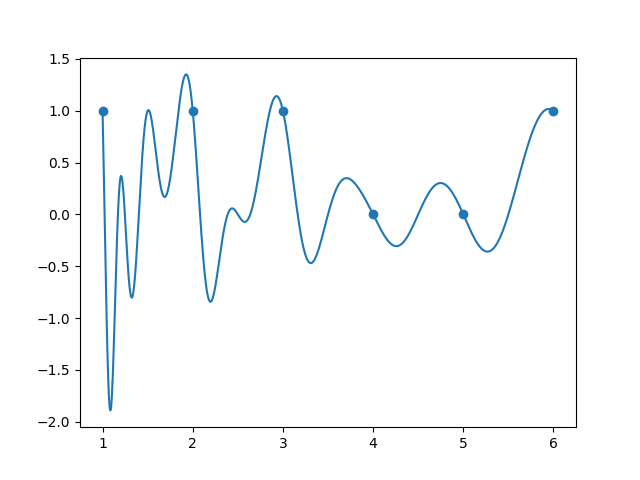
The next example explores ( n = 8 ):
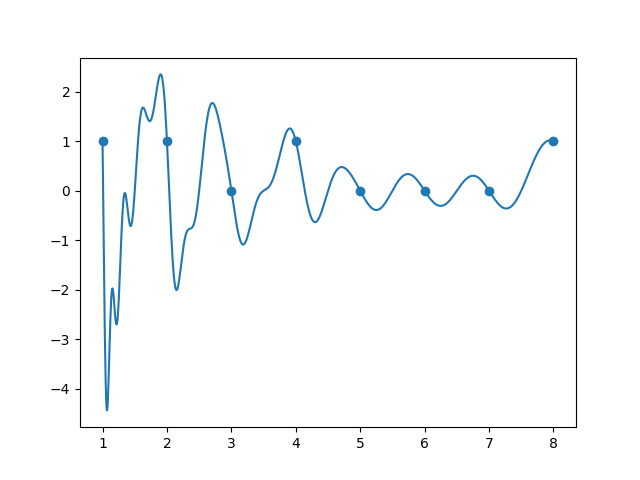
This approach appears promising. Now, we can sum these values to derive the divisor functions through integrals. Returning to our complex function, we can define divisor functions by employing ( d ).
Chapter 2: Implications in Number Theory
We note that when ( a = 0 ), the function counts the divisors of a number. When ( a = 1 ), we arrive at the sum of divisors, a significant concept in number theory. A brief check with Python confirms that our examples and the graphs for the sum of divisors align correctly.
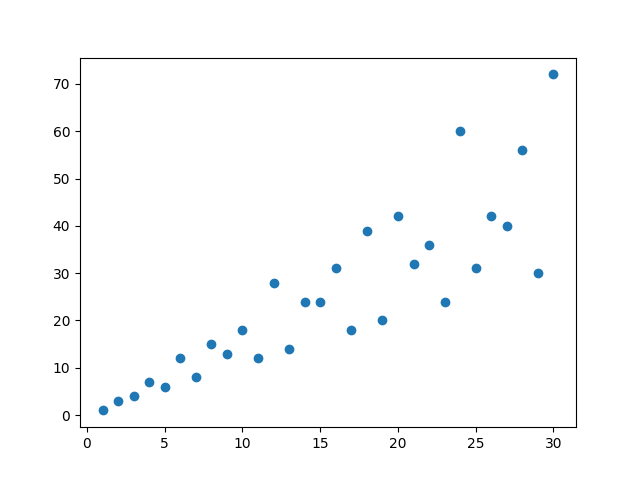
In particular, this function returns 2 only when ( n ) is a prime number, allowing us to effectively identify primes through our complex exponential approach.
For example, let’s denote the prime counting function, which counts primes less than or equal to a real number ( x ), as ( pi(x) ):
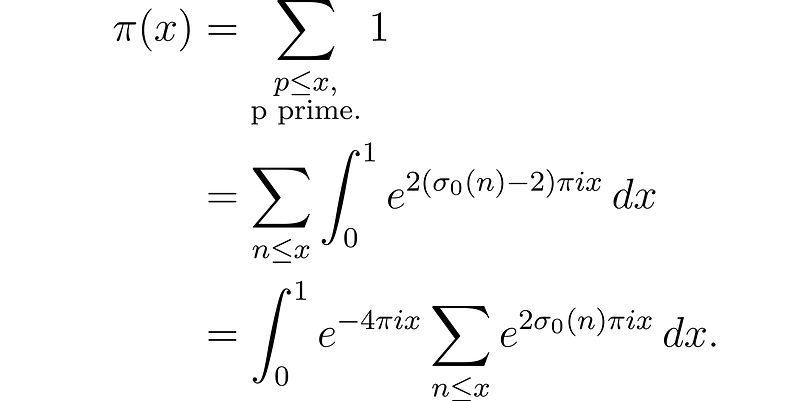
We could substitute our formula for ( pi_0 ) into this expression and utilize the Abel summation technique to make ( pi_0 ) differentiable. I encourage readers to explore this further, along with necessary Python validations.
As we conclude this article, I’m excited to continue refining these formulas, potentially leading to a "part 2" in the future. Thank you for reading!
This video, titled "How to use Python to Check for Prime Numbers!" provides practical insights into using Python for prime detection.
In this second video, "Simple Primality Test - Check if a number is prime in Python," we delve into straightforward methods for testing prime numbers using Python.