Chapter 1: Understanding the Hexagonal Configuration

Consider a convex hexagon ABCDEF where the diagonals AD, BE, and CF intersect at point O. For any triangle XYZ, denote its area as [XYZ]. It is given that [OAF] represents the geometric mean of [OAB] and [OEF], while [OBC] is the geometric mean of [OAB] and [OCD]. Your task is to demonstrate that [OED] is the geometric mean of [OCD] and [OEF].

To assist in understanding, please refer to the accompanying Theorem Grid for the relevant theorems that will be utilized throughout this proof.

Section 1.1: Strategies for Area Calculation

This problem revolves around the areas of triangles, and since we lack height measurements, Theorem 1.7 emerges as a suitable starting point. We will express the area of each triangle using an angle and the lengths of two of its sides. The question now is which angles and sides to select?

To simplify our calculations and minimize the number of variables, we will focus on the angles around point O and the shared sides among triangles OA, OB, OC, OD, OE, and OF.

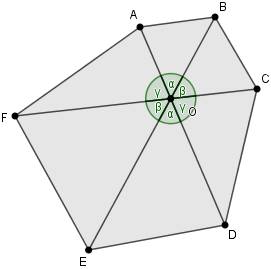
By applying Theorem 1.7, we can express the relationships accordingly.

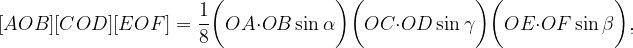
Thus, we arrive at the equation [AOB][COD][EOF] = [BOC][DOE][FOA]. We will refer to this equation as (*).

Section 1.2: Incorporating Given Conditions

Now, we need to integrate the problem's conditions into mathematical equations.

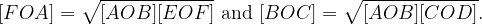
When we combine these with equation (*), we find that

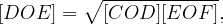
which aligns perfectly with our objective.

Chapter 2: Conclusion and Insights

In the realm of problem-solving, starting with simple concepts is often the best approach. Moreover, knowing which mathematical tools to apply is crucial for success. This skill, however, is not easily acquired; it typically develops with experience. In this exercise, we have illustrated the reasoning process involved in approaching a geometric problem by utilizing the available tools effectively.