The Concept of Orthogonal Functions and Generalized Fourier Series
Written on
Chapter 1: Understanding Orthogonality in Geometry
Orthogonality is a concept that many of us first connect with the idea of perpendicular lines in geometry. When two vectors are orthogonal, they intersect at a right angle (90 degrees). This fundamental notion serves as our starting point.
In this piece, we will delve into a remarkable concept from advanced calculus: the expansion of orthogonality to functions, culminating in what is known as the Generalized Fourier Series.
Let’s get started!
Section 1.1: A Brief Review of Vectors
Before we explore the details of orthogonal functions, let's revisit the essentials of vector analysis. Imagine two vectors in three-dimensional space.
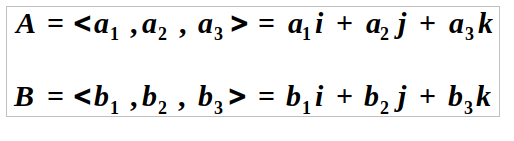
Here, we denote the standard basis vectors as:
- i = <1, 0, 0>
- j = <0, 1, 0>
- k = <0, 0, 1>
The magnitude of a vector ||A||, also known as its norm, is determined as follows:
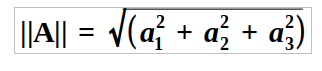
We define the inner product of two vectors, A and B, with the equation:
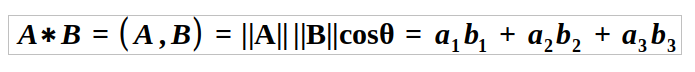
In this formula, θ represents the angle between the two vectors shown above. If two vectors are orthogonal (perpendicular), their inner product will equal zero since cos(90°) = 0.
A collection of n vectors is termed an orthogonal set when each vector is perpendicular to all others. Furthermore, if all vectors in the set have a norm of 1, we call it an orthonormal set. For instance, the set {i, j, k} = { <1, 0, 0>, <0, 1, 0>, <0, 0, 1> } is an orthonormal set, as demonstrated below.

Now that we have refreshed our memory, let’s examine how we can broaden the idea of orthogonality to functions.
Section 1.2: Introducing Orthogonal Functions
Consider a function A(x) defined over the interval a ≤ x ≤ b. One way to visualize A(x) is to think of it as a vector with an infinite number of components, where each component corresponds to the value of A(x) at a specific x within the range (a, b).
With this analogy established, we can apply concepts from vector analysis to functions. For instance, the norm of a vector is found by taking the square root of the sum of the squares of its components. We extend this concept to functions with the following definition of the norm:
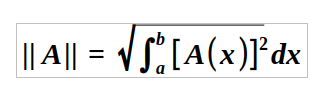
Observe how this definition mirrors that of a vector's norm, differing only in that we replace the sum with an integral, given the infinite nature of the components.
Next, we define the inner product of two functions, A(x) and B(x), as follows:
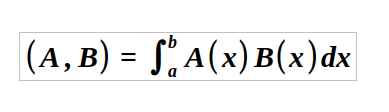
Take a moment to reflect on why this definition is logical. In vector analysis, the inner product is the sum of the products of corresponding components. The formula above captures this idea and extends it to functions by substituting the sum with an integral.
To maintain the analogy, A(x) and B(x) are considered orthogonal if:
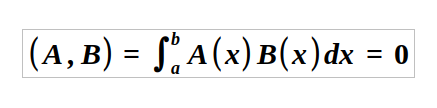
A set of functions is orthogonal if every function is orthogonal to all others. If the norms of the functions equal 1, we refer to the set as orthonormal.
Given a set { f_n(x) } of orthonormal functions:
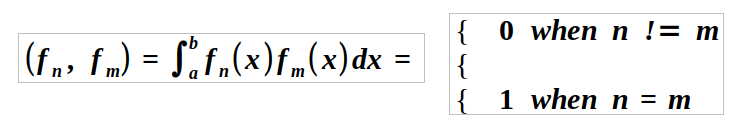
Lastly, note that a set { f_n(x) } can be converted to an orthonormal set by dividing each function by its norm ||f_n|| if it is orthogonal but not orthonormal.
Chapter 2: The Role of Weight Functions
We can extend our definitions by introducing weight functions. The orthogonality of a set of functions {f_n(x)} can be generalized to include a weight function r(x) > 0 as follows:
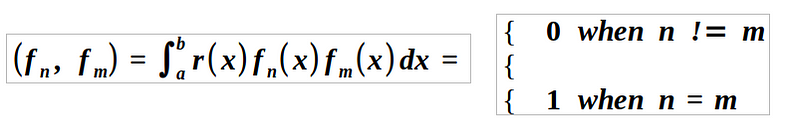
The norm of a function is then expressed as:
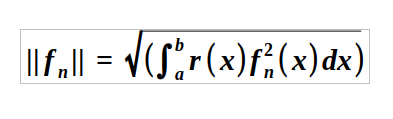
One can quickly see that traditional orthogonality occurs when r(x) = 1.
Section 2.1: Series of Orthogonal Functions
Most learners will remember the Taylor series from their early calculus studies, which illustrates how a function can be represented as an infinite weighted polynomial. Interestingly, we can express a function as an infinite series of orthogonal functions.
Consider the set { g_n(x), n ∈ N }, defined over the interval a ≤ x ≤ b, which is orthogonal relative to a weight function r(x). For a specific function f(x), we can write:
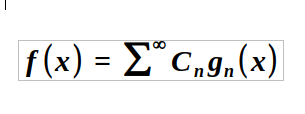
Note: We assume the series converges uniformly.
To determine the coefficients C_n, we multiply both sides by r(x)g_n(x) and integrate over the interval [a,b]:
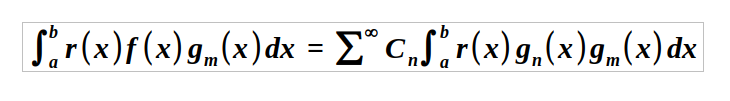
Recalling the orthogonality property, all terms in the series vanish except when n = m, leading to:
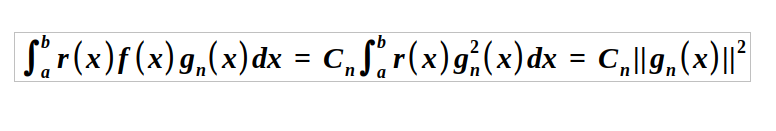
Solving for C_n gives us:
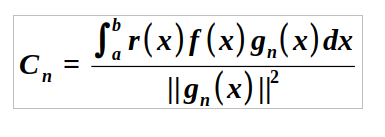
This formulation for f(x) is referred to as an orthonormal series or a generalized Fourier series, with the coefficients C_n identified as the Fourier coefficients.
Interestingly, for a periodic function with angular frequency ω, the orthogonal functions take the form of complex exponentials:
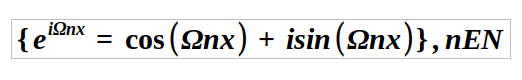
Final Thoughts
This concept is a crucial result in mathematics. The generalized Fourier series is invaluable for decomposing functions into simpler components, which aids in solving numerous problems in various fields such as physics, mathematics, and engineering.
One lingering question remains: How do we identify these orthogonal function sets? To explore this, we must investigate a specific category of problems known as Sturm-Liouville problems, which hold significant importance in differential equations. But that's a discussion for another day…
Thank you for reading, and keep your curiosity alive! If you have suggestions or requests for future articles in the "Intuition behind..." series, feel free to leave a comment or reach out.
You can access all stories on Medium for just $5/month by signing up through this link.