Understanding the Problem

Recently, I came across a thought-provoking question in an article:

"Imagine you are positioned on an infinite grid in a two-dimensional space. While you have an unobstructed view in all directions, your line of sight is blocked by grid points. What proportion of these grid points are visible to you?"

This question is intriguing because it remains unaffected by your starting location, and intuitively, it seems reasonable that you cannot see through other grid points. However, we need to clarify our understanding since there are infinite visible and non-visible points. How do we define their ratio? What constitutes the grid?

For our purposes, let's define the grid as integer coordinate points, (x,y), where both x and y are whole numbers. Without losing generality, we can position ourselves at the origin, (0,0).

The Problem Explained

To illustrate the issue, consider yourself at the origin (0, 0). In this case, a point like (4, 9) is visible since no other point obstructs your view.

This scenario is demonstrated in the following figure:

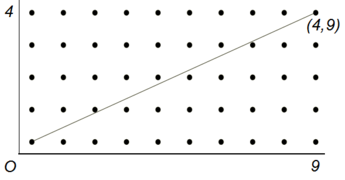
Conversely, the point (6, 2) is not visible because (3, 1) lies directly in your line of sight. Upon reflection, it becomes clear that both points share a common line that passes through (0, 0). Thus, one point must be a multiple of the other, which means their coordinates must have a greatest common divisor (gcd) greater than 1. Mathematically, we express this as gcd(x, y) > 1.

This reasoning allows us to reformulate our question.

Counting Visible Points

Let's draw a square around the origin with side lengths of 2r and count how many points within this square are visible. We then divide this number by the total number of points inside the square for each value of r. This creates a function CP(r) to analyze.

To clarify, we define C(r) as the number of coprime pairs within the 2r-square divided by the total number of points within that square. Our inquiry now focuses on the limit of CP(r) as r approaches infinity.

To visualize this concept, we can utilize Python code to examine the results.

# Sample Python code to calculate visible points

...

Upon executing this code, you will receive two outputs. The first will indicate:

"The fraction of visible points with r = 1000 is approximately: 0.60798." The second output will present a convergence graph:

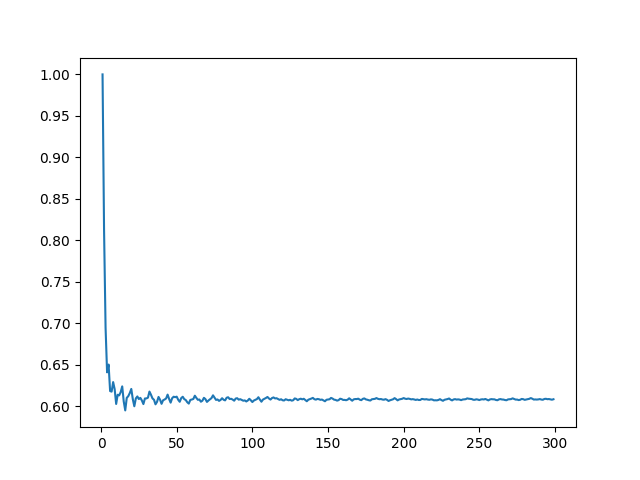
From this data, we can deduce that roughly 60.79% of the points are visible when standing at the origin. By slightly adjusting the code, we can also visualize the distribution of visible points in one quadrant:

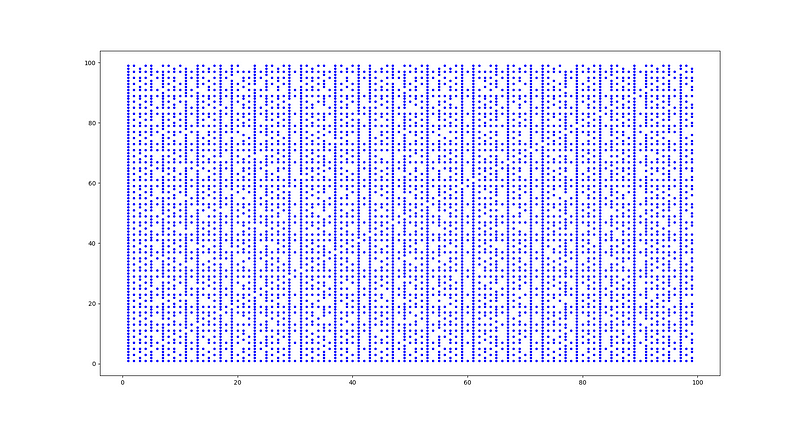
Notice how the density of points in a vertical line correlates with their primality: denser lines indicate more prime numbers, while sparser lines suggest composite numbers. Can you identify the twin primes between 1 and 100 in this image?

A Probabilistic Perspective

Let’s consider this problem through a probabilistic lens. We want to determine the likelihood of selecting a visible point when r is considerably large.

The probability of choosing a visible point, or a coprime pair P = (x, y), equals the chance that no prime divides both x and y.

We can instead compute the complement of this event: "What is the probability that a chosen point is not visible?" For this to occur, at least one prime must divide both coordinates x and y. The chance that a specific prime divides x is 1/p, and similarly, for y, it’s also 1/p. Assuming independence, the probability that both x and y are divisible by p is 1/p².

Consequently, the probability that p does not divide both coordinates, and hence that the point (x, y) is visible, is given by the product:

P(text{visible}) = prod_{p text{ prime}} left(1 - frac{1}{p^2}right)

This can be expressed more compactly:

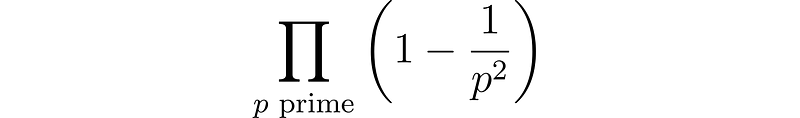
When expanded, this product leads us to a series of numbers of the form 1/m², where m is square-free (no square divides m) and whose prime factorization consists only of distinct primes. The sign of each term is determined by the count of distinct prime factors: an odd count yields a negative term, while an even count yields a positive term.

This function is known as the Möbius function, denoted by μ. From our analysis, we derive:

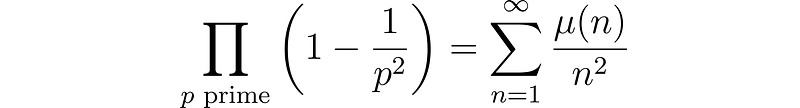
The series begins as 1 – 1/2² – 1/3² – 1/5² + 1/6² - 1/7² + ... Adding these six numbers results in approximately 0.606, which is quite close!

The Significance of This Number

What does this particular number signify? Can we express it in a closed form?

Interestingly, this expression equates to 1/ζ(2), where ζ denotes the Riemann zeta function. Euler demonstrated that ζ(2) = π²/6. Thus, we conclude that the proportion of visible points is exactly 1/ζ(2) = 6/π², which approximates to 0.6079271...

The Riemann zeta function is defined as:

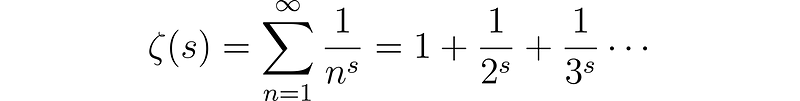
for s > 1, having been extensively studied by Euler in the 1700s. A century later, Riemann explored this function in the context of complex variables, revealing its profound beauty.

Euler discovered a remarkable product formula for the zeta function, analogous to the fundamental theorem of arithmetic:

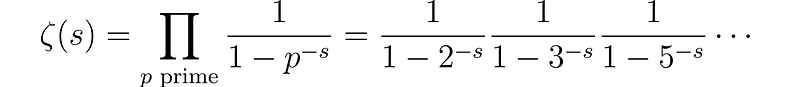
for s > 1. When we raise this product to the power of -1 and set s = 2, we derive exactly our expression for 1/ζ(2).

Extending to Three Dimensions

What if we extend this inquiry into three-dimensional space?

By applying similar reasoning, one can demonstrate that the fraction of visible points in a 3D grid is 1/ζ(3). This constant is enigmatic in mathematics, as no one has yet uncovered a closed-form representation. The individual who achieves this feat may achieve worldwide recognition.

Explore the depths of the Riemann zeta function and its analytic continuation in this insightful video.

Delve into the elegant argument surrounding the Riemann zeta function and its profound implications in mathematics.