Events and Reference Frames

At its core, an event in spacetime is an occurrence that can be assigned a set of coordinates. For this discussion, we will employ traditional Cartesian coordinates (x, y, z) to describe our spatial dimensions. A frame of reference can be understood as a system for assigning these coordinates to events, equipped with synchronized clocks at every point. This allows us to assign a time coordinate (t) alongside the spatial ones.

This frame of reference, depicted in two spatial dimensions, contains synchronized clocks. When an event occurs at a specific location, it can be assigned both a time by a local observer and spatial coordinates.

A crucial category of reference frame in our exploration of Special Relativity is the inertial frame. Defined by the adherence to Newton's First Law of motion, inertial frames are those moving at a constant velocity without acceleration (including rotation).

Interestingly, for every inertial frame, an infinite number of such frames exist, all moving at constant velocity relative to one another. A fascinating outcome of this relationship is that just because one event occurs before another in one frame, it doesn't imply the same order in all frames.

Introducing Our Observers: Zip and Zip Prime

These frames would lack excitement if they were void of content. Therefore, we introduce our inertial observers, each navigating their own reference frame. They are committed to documenting events within their respective frames.

Our first observer, Zip, is a scientist from our universe who has created a platform enabling him to travel at speeds close to light without concerns about friction or energy. This platform facilitates various experiments to investigate the implications of Special Relativity.

However, during one of his initial journeys, Zip inadvertently tears through spacetime, bringing forth his alternate counterpart, Zip Prime. This equally ambitious duplicate possesses a remarkable platform of his own.

With our inertial frames and their inhabitants established, we can now examine how coordinates transform between these frames, both at low speeds and when Zip and Zip Prime approach relativistic speeds, comparable to c—the speed of light.

Coordinate Transformations and the Lorentz Factor

As the name suggests, a theory of relativity focuses on the relationships between observations made by observers in relative motion. We will analyze Zip’s frame (S) aligned with Zip Prime’s frame (S’). The designation 'S prime' indicates that this frame belongs to Zip Prime. In standard configuration, the y-axis and z-axis of both frames are parallel, and the origin (0, 0, 0) of S' moves along the x-axis of S with a relative velocity denoted as V.

Let's visualize what this looks like.

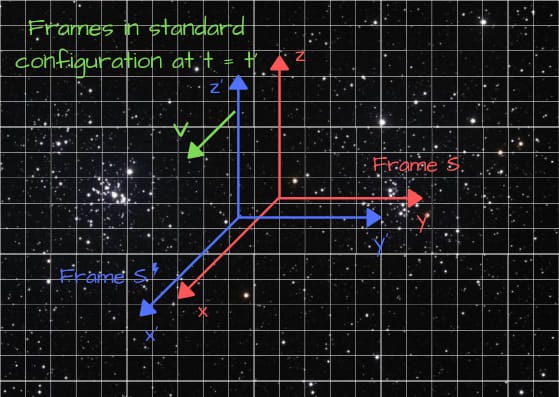
When velocities (V) are much slower than c, the transformations between these frames become straightforward.

The first equation suggests that time is absolute—the time interval between two events remains constant for all observers—contradicting the tenets of Special Relativity.

Einstein recognized the need to reformulate these transformation rules to align with his two postulates, particularly the constancy of light speed. Fortunately, a colleague had already established the precise set of transformations he required.

The Lorentz Factor—A Key Element

The conclusions Einstein reached while reevaluating the transformation rules matched a set of equations previously derived by Dutch physicist Hendrik Lorentz. Lorentz's transformations emerged from his analysis of Maxwell's laws of electromagnetism. This connection is vital to the narrative of relativity and must have thrilled Einstein.

The very inquiry that spurred Einstein's exploration of light and its speed stemmed from Maxwell's electromagnetism, which seamlessly integrated electricity and magnetism. Maxwell discovered that electromagnetic waves traveled at 3.0 x 10^8 m/s, precisely the speed of light. Einstein recognized this was no coincidence.

The transformations derived by Lorentz and later utilized by Einstein differ from traditional equations, indicating a 'mixing' of time and space, with the t' coordinate now reliant on both x and t. Consequently, two observers may not concur on the timing of an event, which means time is not absolute.

You can almost sense the unease in the established principles of physics.

The Lorentz transformations, though seemingly complex, can be deciphered through a numerical factor that pervades relativity—the Lorentz factor, symbolized by the Greek letter gamma (γ). This factor is often represented as γ(V) to highlight its dependence on the relative velocity between frames.

For speeds significantly lower than that of light, the Lorentz factor approaches 1 (γ(V) ≈ 1). Thus, at slower velocities, Lorentz transformations closely resemble conventional transformations. The following graph illustrates this behavior.

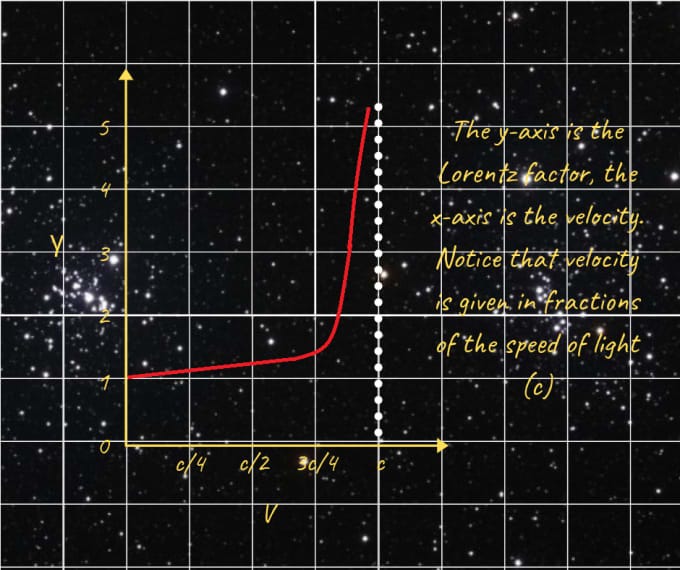
As depicted, the Lorentz factor escalates rapidly as speed nears that of light.

What Lies Ahead?

Equipped with this foundational understanding of relativity, the question arises: what comes next?

In the following discussion, we will delve into the fascinating effects of time dilation as Zip and Zip Prime embark on an extraordinary journey to nearby galaxies, only to return to a world forever changed.

The first video titled "Special Relativity: Frames of Reference" offers an insightful overview of the essential concepts of reference frames in the context of Special Relativity.

The second video, "Easy Way to Understand Special Relativity | Lorentz Transformation | Time Dilation," provides a comprehensive explanation of Lorentz transformations and the phenomenon of time dilation.

Sources and Further Reading

• Relativity, Gravitation and Cosmology (Lambourne, 2012, Cambridge Press)
• Relativity, Gravitation and Cosmology (Cheng, 2010, Oxford University Press)
• Relativity: A Very Short Introduction (Stannard, 2008, Oxford University Press)
• Special Relativity and Classical Field Theory: A Theoretical Minimum (Susskind, Friedman, 2017, Allen Lane)

Originally published at Vocal