# Understanding Game Theory: Nash Equilibria and Pareto Efficiency
Written on
Chapter 1: Introduction to Nash Equilibria
In the previous chapter, we explored Nash Equilibria, which represent scenarios where no player can improve their outcome by changing their strategy alone. Take, for instance, the well-known Prisoner’s Dilemma. The sole Nash Equilibrium occurs when both players choose to defect:
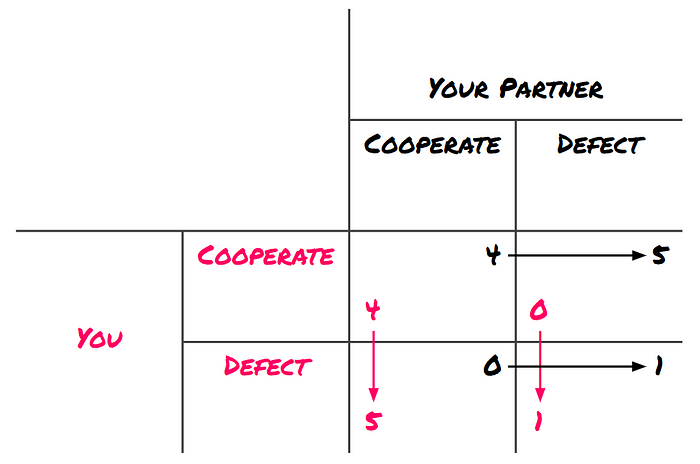
The Prisoner's Dilemma
It's essential to highlight two key aspects of this Nash Equilibrium: first, it results in a highly unfavorable outcome, as there exists a preferable scenario (cooperate vs. cooperate) for both players; second, it illustrates a "logical" conclusion, as each player is following a dominant strategy. This combination is rarely advantageous.
However, not all Nash Equilibria are detrimental. Let's consider the Battle of the Sexes scenario.
Section 1.1: The Battle of the Sexes
Alice and Chris plan to attend an event together, but due to Chris losing his phone, they cannot communicate about their destination. Earlier discussions included both a boxing match and a ballet performance. While Chris favors the boxing match, Alice prefers the ballet. Ultimately, both would rather attend either event together than go solo to their preferred one. Which event should they choose?
The payoff matrix for this scenario is as follows:
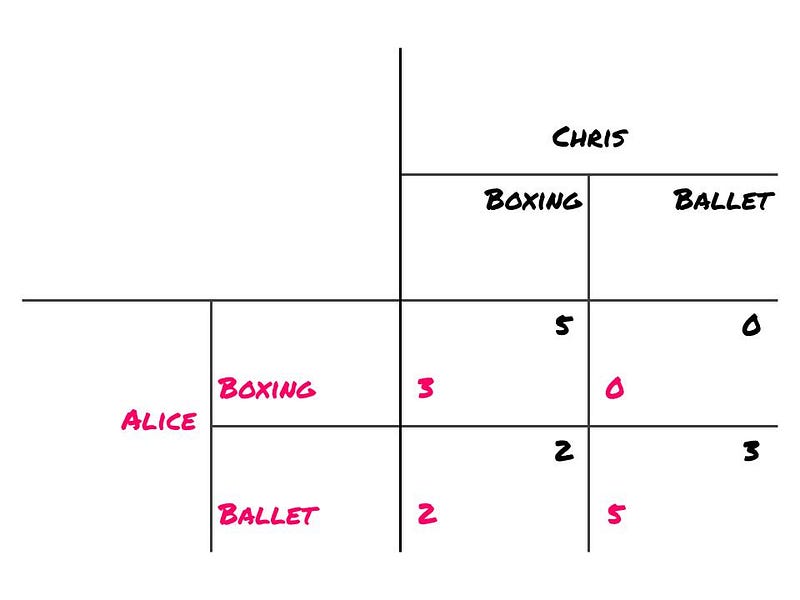
Payoff Matrix Analysis
Alice and Chris agree that the least desirable outcome is when Alice attends the boxing match while Chris goes to the ballet. If they opt to attend their preferred events separately, they at least gain some utility. The two scenarios where both attend the same event represent Nash Equilibria: in these cases, if either were to switch events, they would experience a decrease in utility.
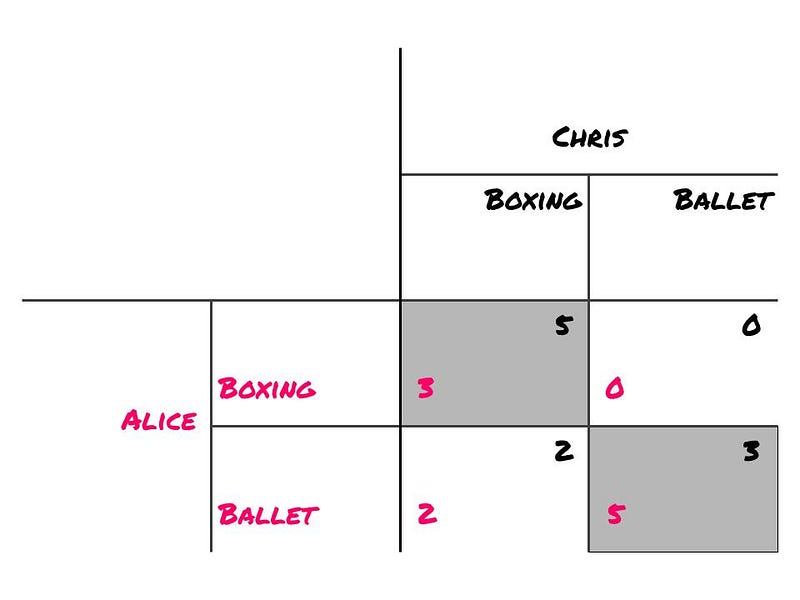
Section 1.2: Pareto Efficiency in Nash Equilibria
What’s notable about these particular Nash Equilibria is their status as Pareto Efficient: no alternative exists that can improve one player’s outcome without harming the other. These Nash Equilibria represent the most favorable outcomes in the game.
Achieving Pareto Efficiency can be viewed as a fundamental goal for any game's results. If a scenario benefits one player without disadvantaging another, it stands to reason that this outcome is preferable.
The significant issue with the Prisoner’s Dilemma is that every result apart from the Nash Equilibrium is Pareto Efficient. Consequently, rational and self-interested players often find themselves in a suboptimal situation (which is detrimental to both!).
In certain scenarios, it is possible to evade poor Nash Equilibria through strategic thinking. More on this topic will be addressed in the next chapter!
If you’re interested in supporting Street Science, consider contributing on Patreon.
Chapter 2: Practical Applications of Game Theory
In this video titled "Game Theory Dominant Strategy Practice: Econ Concepts in 60 Seconds," viewers will gain a quick overview of dominant strategies within game theory, enhancing their understanding of the concepts discussed.
The second video, "Intro to Game Theory and the Dominant Strategy Equilibrium," provides an in-depth introduction to game theory, focusing on dominant strategy equilibria and their implications.