Chapter 1: The Playful Side of Mathematics

Mathematics, often viewed as a serious discipline, has its fair share of whimsical terminology that adds a lighthearted touch to its abstract concepts.

Quoting from the humorous perspective of mathematics, we can say that while there are numerous abstract concepts, the names we assign to them often evoke laughter or curiosity. For instance, the 'hairy ball theorem' is an example of a mathematical result named after a tangible scenario, which we will delve into shortly.

Section 1.1: The Unconventional Naming Conventions

The natural numbers are represented by the letter N, the rational numbers by Q (for quotient), the real numbers by R, and the complex numbers by C. But why do we use Z for integers?

The answer lies in the German word ‘Zahlen’, which translates to numbers. Although one might think that integers could be denoted by I, that letter is already taken for irrational numbers. Mathematicians often prefer to express the irrational numbers as RQ, conserving chalk in the process.

Subsection 1.1.1: Fields and Their Odd Names

A 'field' encompasses a set of elements that can undergo addition, subtraction, multiplication, and division while adhering to specific properties. This concept aptly describes the rational (Q), real (R), and complex (C) numbers.

The notation K is often used to represent an arbitrary field, derived from the German word ‘Körper’, which translates to ‘body’ rather than ‘field’.

Interestingly, the definition of a field introduces some peculiar collections, like the 2-element field {0, 1}. In this field, the equation 1 + 1 = 0 holds true, humorously showcasing how it functions as a field. I recall needing to preface many linear algebra results with the phrase “Assume that 1 + 1 ≠ 0,” which always made me chuckle.

Section 1.2: The Hairy Ball Theorem

The 'hairy ball theorem' is a classic in algebraic topology and is one of my personal favorites. It states that on even-dimensional n-spheres, one cannot create a non-vanishing continuous tangent vector field.

To visualize this, think of a 2-sphere, or simply a sphere, akin to the surface of a ball. The theorem suggests that one can never comb hair on a sphere without leaving at least one strand standing up.

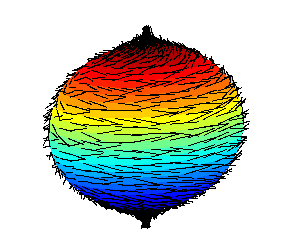
This theorem humorously illustrates how an abstract concept can be named after a relatable scenario. Additionally, it applies to higher-dimensional spheres, such as 4-spheres and 6-spheres, hinting at an amusing reality about wind patterns on Earth—there’s always at least one spot without wind.

Chapter 2: The No-Hair Theorem

The 'no-hair theorem' continues the theme of hair in mathematics. It asserts that stationary black holes can be fully characterized by three observable characteristics: mass, electric charge, and angular momentum.

This means that all other properties of a black hole are uniquely determined by these three metrics, with the term 'hair' referring to any additional attributes that are not part of the theorem.

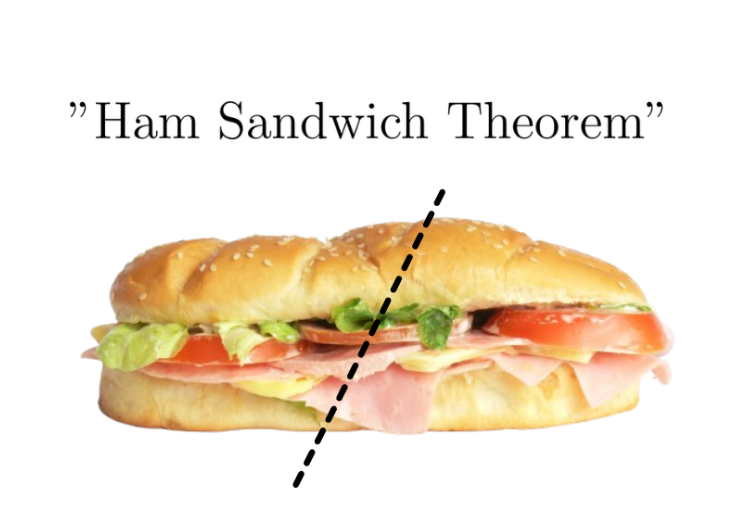
Chapter 3: The Ham Sandwich Theorem

The 'ham sandwich theorem' states that given n objects in n-dimensional Euclidean space, there exists a (n-1)-dimensional hyperplane capable of bisecting all n objects simultaneously.

This theorem gets its name from its application to a ham sandwich, which comprises three components: two slices of bread and a slice of ham. Regardless of how the sandwich is configured, one can always slice through it with a single planar cut.

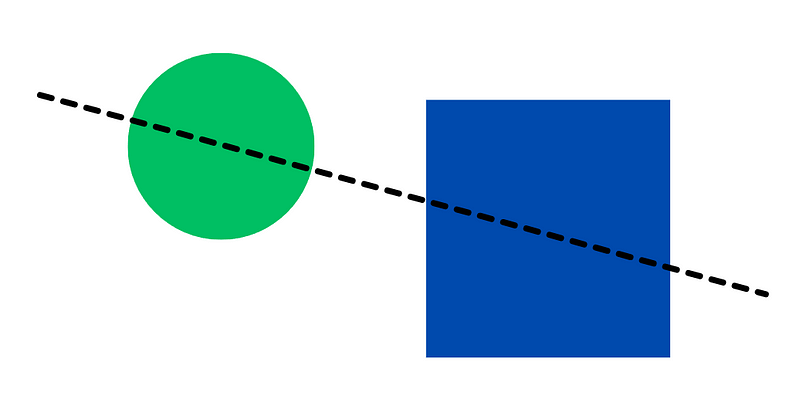
For those preferring a vegetarian option, the following theorem might be more appealing.

Chapter 4: The Sandwich Theorem

The 'sandwich theorem' emerges from real analysis and pertains to convergent sequences. It posits that if a sequence is bounded between two other converging sequences that share the same limit, then it too must converge to that limit.

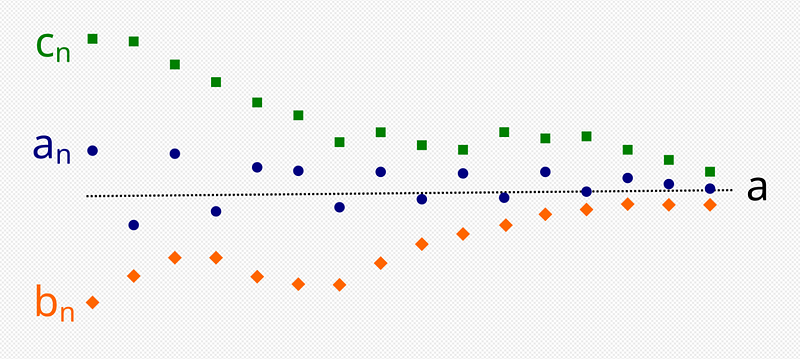
This theorem is affectionately termed the sandwich theorem, also known as the squeeze theorem for similar reasons, though I favor the former title.

Finally, we have the Cox-Zucker Machine, which, while I cannot accurately explain its function, relates to elliptic surfaces. The name was intentionally chosen by David A. Cox and Steven Zucker, adding a layer of humor to the serious nature of mathematical study.

If you have any quirky or humorous mathematical terms to share, please feel free to comment below!

The second video titled "Crazy Math Patterns that stop working...eventually" explores the fascinating and sometimes unpredictable nature of mathematical patterns, offering insights and laughter along the way.