The Optimal Positioning of a Prison Guard: A Mathematical Inquiry
Written on
Chapter 1: Understanding the Problem
In the realm of mathematical challenges posed by Cambridge University, we encounter a thought-provoking problem: "Where should the prison guard be?" This problem seamlessly blends geometry with calculus.
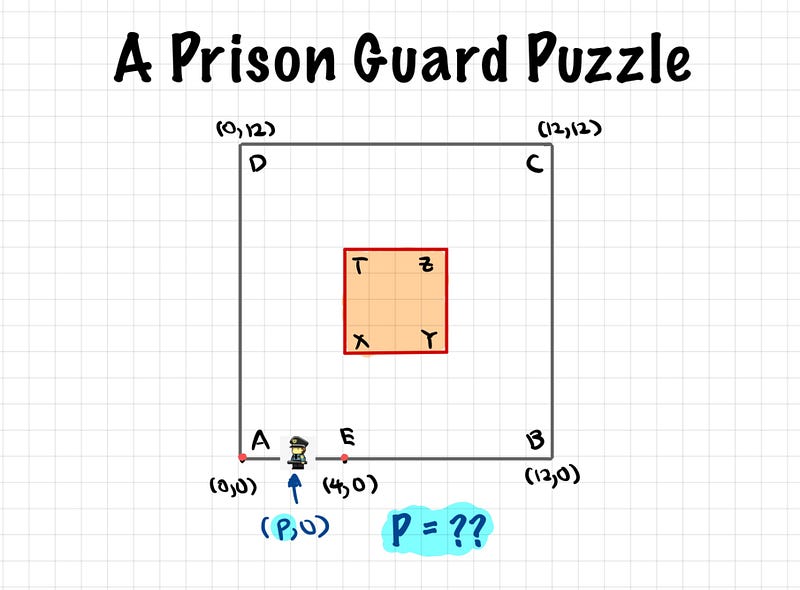
The scenario presents a guard patrolling from point A to point E, and our task is to ascertain the position P where the guard can observe the maximum area, as well as where he can observe the minimum area.
While exploring some of the STEP (Sixth Term Examination Papers) problems from Cambridge, I came across this elegant challenge from 1991. Even after more than three decades, it remains a stimulating exercise!

Cambridge STEP Problem 4 (1991): The goal is to determine the values of P that fulfill parts (a) and (b) of the question. Here, P represents an arbitrary position where the guard stands. How would one approach solving this problem?
The mathematics involved is accessible to any high school student, as it is based on fundamental calculus principles. Nevertheless, there is a wealth of creativity and enjoyment to uncover.
This exposition might take a bit longer than usual, as it took me approximately 40 minutes to derive the solution, but I assure you, the effort will be worthwhile. Here’s a tip: utilize diagrams extensively!
I encourage you to pause and engage with the problem using pen and paper before continuing to the solution.
Solution Strategy
It’s often beneficial to analyze the boundary conditions in a problem. In our case, let’s consider the guard’s visibility from points A(0,0) and E(4,0). I will be employing a grid system for clarity, although precise coordinates can be determined through calculus.
Be mindful of the tower obstructing the guard's sightline.
At position A(0,0), the guard perceives the area highlighted in blue.
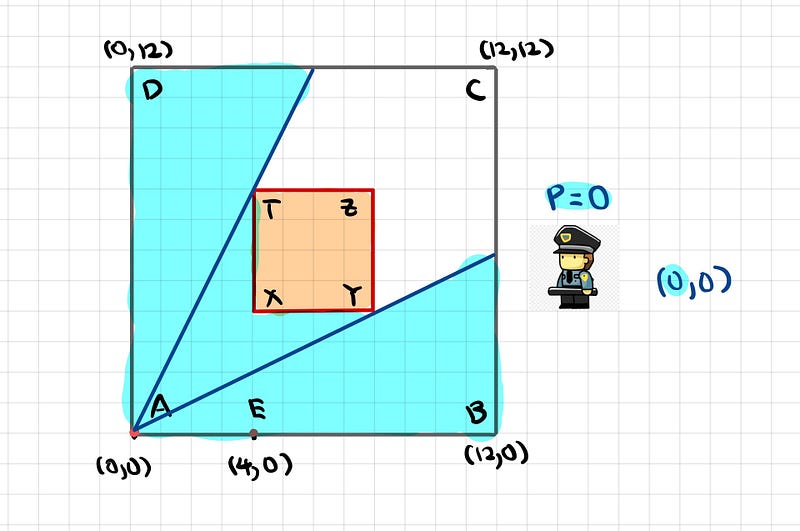
At position E(4,0), the area in green is visible to the guard.
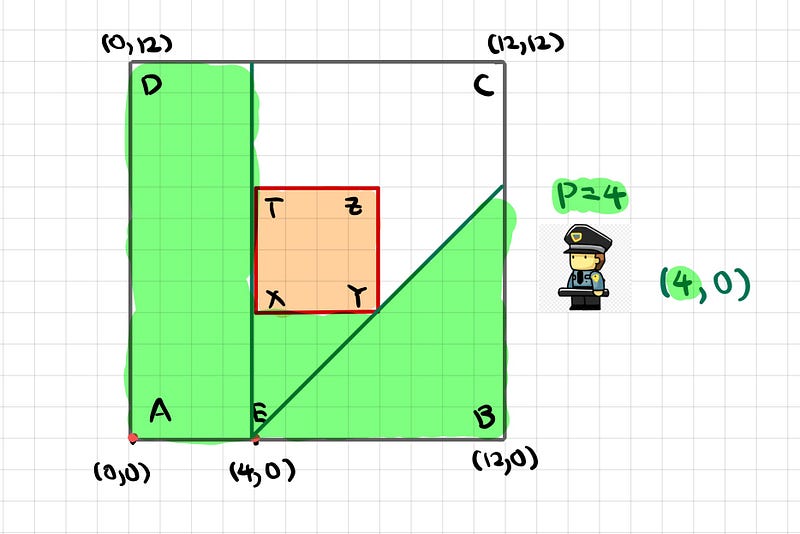
Upon reviewing both diagrams, we observe a significant overlap in the shaded areas. Thus, we can concentrate on the differentiation of these regions to solve the puzzle.
Let's combine the diagrams!
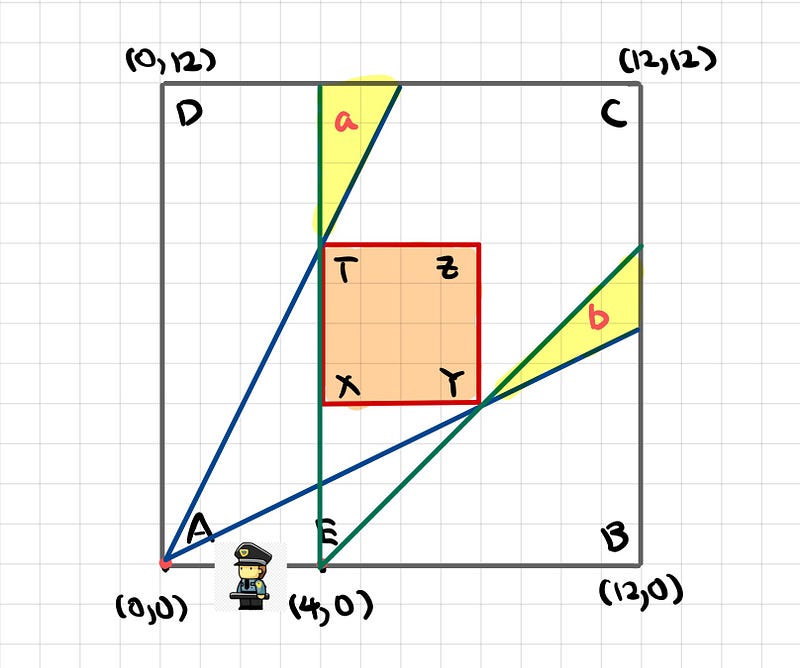
I've highlighted the yellow regions that change as the guard moves between A and E. Visualize the guard projecting two straight rays that touch the corners of the obstructing square. These lines extend until they contact the outer walls of the overall square.
From this visualization, we can deduce that:
- When at A, triangle a is maximized while triangle b disappears.
- When at E, triangle b is maximized while triangle a vanishes.
This critical observation indicates that the guard's position (p, 0) directly influences the area he can observe, which varies with his movement.
Mathematical Modeling
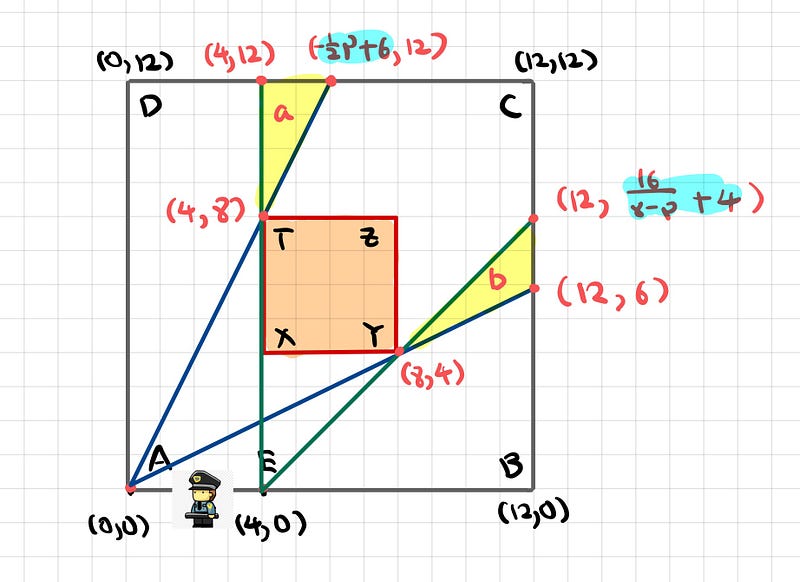
Our next step is to mathematically frame this scenario. Specifically, we aim to express the coordinates of triangles a and b based on the variable p.
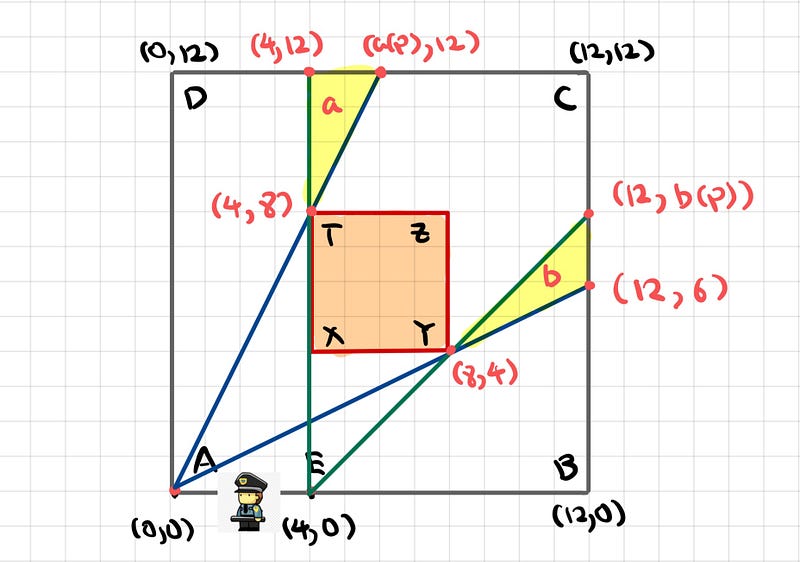
The points marked in red represent the coordinates of the triangles:
- Triangle a consists of points (a(p), 12), (4, 12), and (4, 8).
- Triangle b consists of points (12, b(p)), (12, 6), and (8, 4).
Now, let’s consider an arbitrary position (p,0) of the guard, who will again project two rays defining his field of vision.
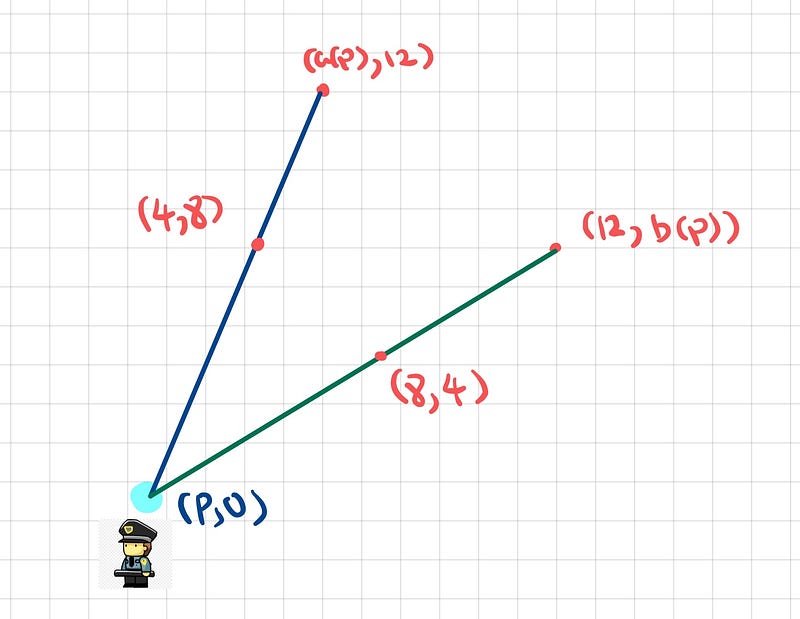
With three points established for each line, our goal is to derive expressions for a(p) and b(p).
Area Calculation
The area of a triangle is calculated as 1/2(b)(h), where b represents the base and h denotes the height. We can apply this formula to triangles a and b.
Triangle a’s area is represented as Delta_a.
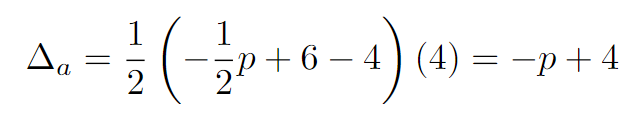
Triangle b’s area is denoted as Delta_b.
Now, by summing the areas of triangles a and b, we derive an expression reflecting the total observable area by the guard as he transitions between A and E.
This results in a function A(p), which quantifies the additional area the guard can see from triangles a and b.
Finding the Optimum with Derivatives
The function A(p) we have formulated is applicable within the range of 0 ≤ p ≤ 4. We will determine the potential optimum point by differentiating this function with respect to p.
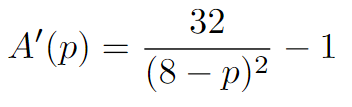
Setting the derivative equal to zero allows us to identify an optimum point.
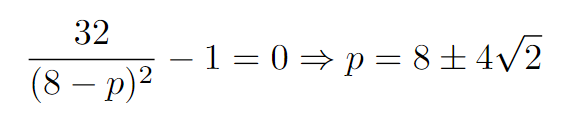
We can disregard the value of 8 + 4√2 as it falls outside the range of interest.
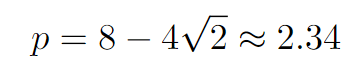
Consequently, we’ve identified an optimum position! By applying the first and second derivative tests, we conclude that this is a local minimum point for A(p). Thus, we have resolved part (a) of the query: the guard has the least observable area when positioned at...
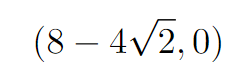
Conclusion to Part (b)
To conclude part (b), we build on the fact that the function reaches a local minimum and that the second derivative remains positive for the range of p from 0 to 4. This indicates that the function exhibits a concave upward shape.
As depicted in the graph below, between 0 and 4, the function A(p) increases as it moves away from the optimal point on either side.
Moreover, it appears that at both endpoints (p = 0 and p = 4), A(p) yields the same outcome, confirming that the guard can maximize visibility from two distinct positions.
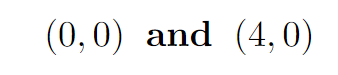
Congratulations! You’ve successfully navigated this mathematical journey. A bonus to ponder: confirm that the maximum area visible to the guard is 88 square units!
What were your thoughts during this exercise? I would love to hear your insights in the comments below!
Math Puzzles: A Treasure Trove
If you’re keen on more intriguing math puzzles, check out this curated list of challenges available on Medium, covering a variety of topics like Algebra, Geometry, Calculus, and Number Theory. Share it with friends for a collective brain workout!
The first video provides valuable insights on surviving as a prison guard, offering practical advice and secrets for navigating life behind bars.
The second video explores whether becoming a correctional officer is the right choice for you, discussing the pros and cons of the profession.
Thank you for your time! If you found this article enlightening, feel free to show your appreciation. Your support helps sustain my writing endeavors.
