Chapter 1: Early Mathematical Curiosities

From a young age, my relationship with numbers began in an unusual way. I received a scientific calculator for my third birthday, a gift that puzzled many, as I was far too young to appreciate it. Initially, it became more of a chew toy than a mathematical tool.

As I grew older, particularly during school trips before the era of iPods, I would bring my calculator on the bus. I found joy in inputting "1 + 1" and repeatedly pressing the equals button, which effectively counted the number of times I pressed it. My friends and I turned it into a game, challenging each other to see how large a number we could create before our stop. Occasionally, we mixed it up with "7 + 7" or "13 + 13" to keep things interesting.

Another playful activity involved typing the digits 1 through 9 into the calculator, resulting in a 9-digit number with each digit appearing exactly once, such as 631598247. These numbers, referred to as "9-digit zeroless pandigital" (or "9DZP") numbers, have a fascinating property: they are always divisible by 9. This divisibility stems from the fact that the sum of the digits from 1 to 9 equals 45, which is a multiple of 9.

I experimented further by dividing these 9DZP numbers by 3 multiple times, hoping to discover how many times I could achieve a whole number result. The most successful instance I remember yielded a number divisible by 3 a total of eight times, including the initial division by 9.

Section 1.1: The Journey into Number Theory

As I matured and developed some programming skills, I revisited this curiosity with a more serious approach. I decided to create a computer program to identify 9DZP numbers that could be divided by the highest powers of 3.

At that time, I had yet to delve into number theory, unaware of the established notation for expressing divisibility by 3:

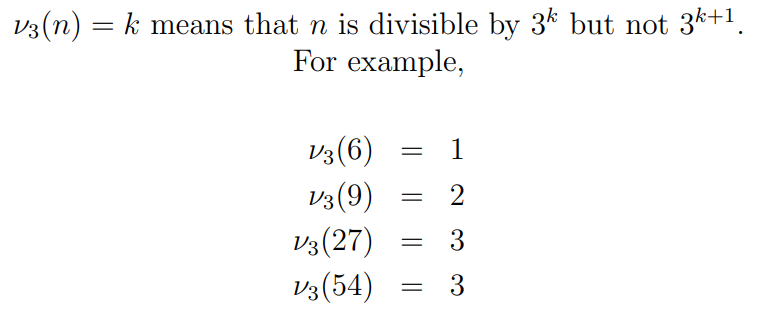
I coined the term "threeven" to describe numbers divisible by 3. For example, 54 has a threevence of 3. My program systematically calculated the threevence of each 9DZP number, tracking how many numbers fell under each category until none remained.

Subsection 1.1.1: Results of the Program

Let ( a(n) ) represent the count of 9DZP numbers with a threevence of at least ( n ). Upon running the program, I discovered that the highest threevence among these numbers is 13, with only two such instances. Had I relied solely on my calculator, I likely wouldn't have stumbled upon these.

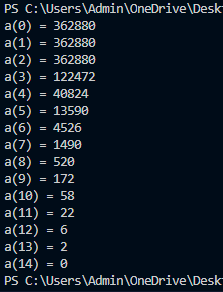
Further analysis revealed that there are a total of 362,880 9DZP numbers, all of which are divisible by 9 and thus possess a threevence of at least 2. This explains why ( a(0) = a(1) = a(2) = 362880 ). While we might expect the counts to decrease by roughly a third with each increase in threevence, the output confirmed this pattern.

Chapter 2: The Discovery of Special Numbers

My program identified the two unique 9DZP numbers with a threevence of 13:

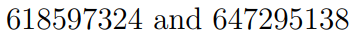
These two numbers, 618597324 (equal to 388 × 3¹³) and 647295138 (equal to 406 × 3¹³), hold a special place in my mathematical journey. I submitted this sequence to the Online Encyclopedia of Integer Sequences, where it has been cataloged as A354708. If you're interested in sequences, I recommend exploring this fantastic resource.

In conclusion, this experience has solidified my commitment to the world of mathematics. I look forward to potentially pursuing a PhD and, perhaps, discovering new sequences along the way.

The first video titled "How Math Saved My Life | Jason Padgett" explores the transformative impact of mathematics on personal experiences, highlighting the emotional and intellectual journeys that can arise from mathematical engagement.

The second video, "Math in the Real World: A Behind-the-Scenes Look (Full Episode)," provides insights into the application of mathematics in various real-world scenarios, showcasing its relevance and importance in everyday life.