Trial and Error with Straight Lines and Triangles

Let's begin by employing a classic trial-and-error method. Initially, we can deduce that constructing a triangle requires at least three lines. Thus, our desired expression should yield zero for cases when n = 0, 1, and 2.

Now, let’s analyze the scenario when we have three lines adhering to the puzzle's conditions:

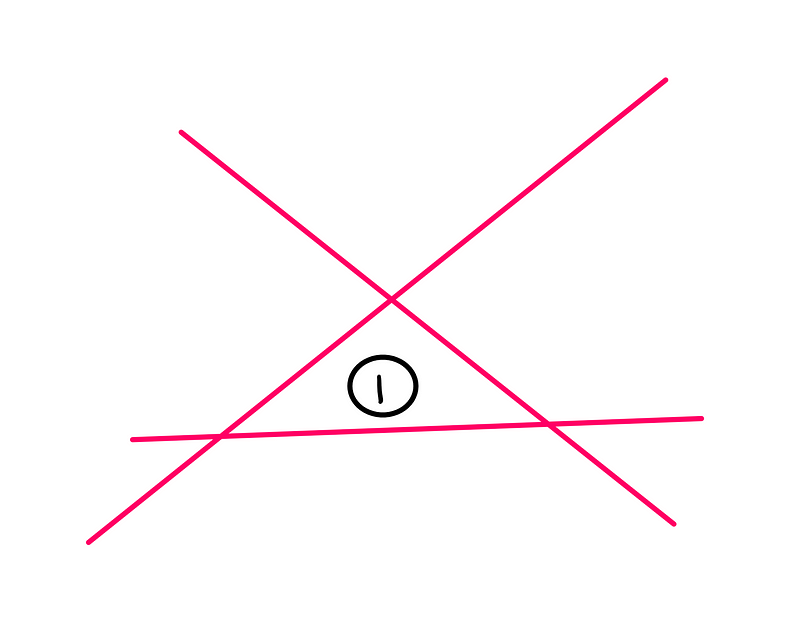
As depicted, we can create exactly one triangle with three lines. Hence, our expression outputs 1 when n = 3. Next, let’s examine the case with four lines:

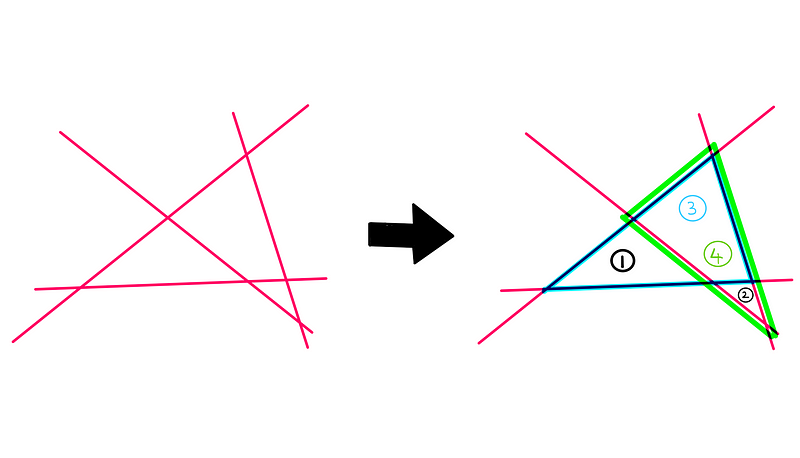
From the illustration, we can form four triangles when using four lines. Progressing further, let's explore the situation with five lines:

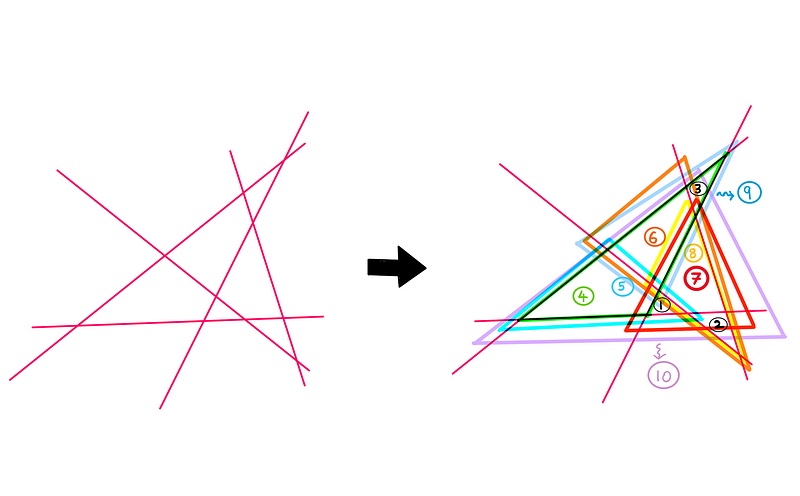
Although this scenario is more complex and chaotic, we conclude that we can form a total of 10 triangles using five lines. While we could continue this process, it becomes increasingly tedious, and we now have enough data to derive a formula.

Using Calculus of Finite Differences to Solve the Puzzle

As previously hinted, we will utilize the calculus of finite differences to uncover the underlying expression. We will begin by compiling our results into an inverted pyramid:

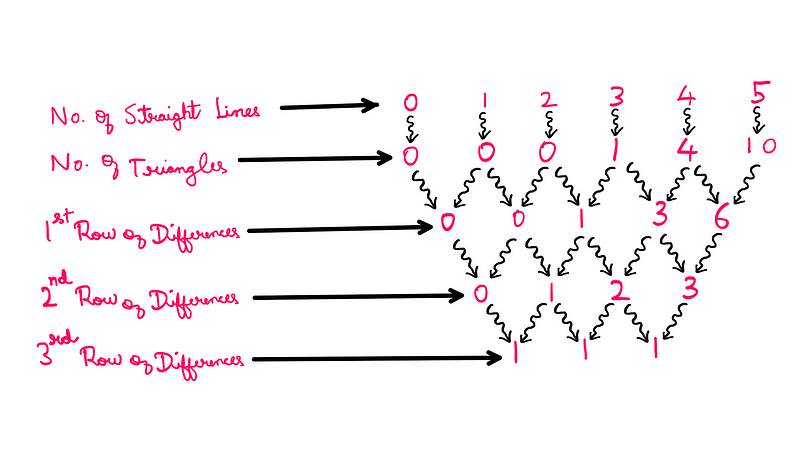
The similarity of the third row indicates that the expression we seek is cubic. If we had observed similar values in the second row, our expression would be quadratic, and linear if in the first. The number of difference rows corresponds to the order of the expression we are investigating.

The Insight of Newton

Fortunately, we have Isaac Newton's formula at our disposal for this method. By denoting the value of the expression for n = 0 as 'a', the first number in the first difference row as 'b', and so forth, we can apply Newton's formula:

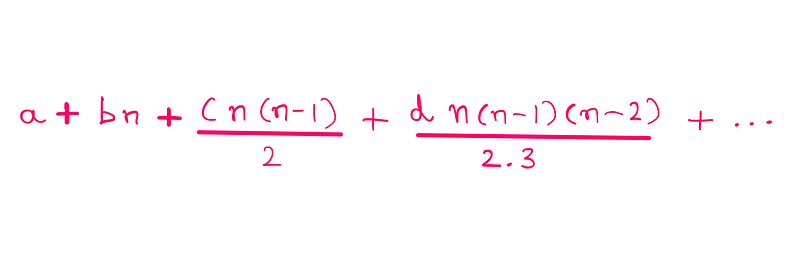
Plugging in our inverted pyramid values yields:

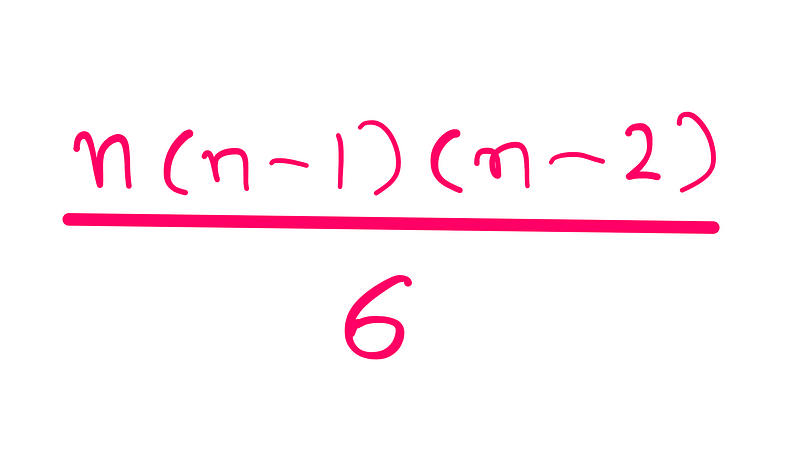
This expression, upon closer inspection, corresponds to the binomial coefficient nC3 (where C represents the combination function in combinatorics). This leads us to the question: How many ways can we select groups of three lines from 'n' total lines?

Why withhold this transformation until now? The purpose is to introduce you to the calculus of finite differences.

A Closer Examination of Finite Differences

To summarize my approach to solving the puzzle:

1. I utilized trial and error to identify patterns in the outputs for sequential inputs.
2. I then applied finite differences to derive a fitting expression.

It’s worth noting that while this method is quite effective, it remains a hypothesis until proven indefinitely valid. The method of differences relies heavily on the observed pattern's accuracy, which can create challenges when applied to real-world scenarios. Often, one data point can invalidate an entire previously established pattern.

As mathematician George Pólya aptly stated:

“Nature may answer Yes or No, but it whispers one answer and thunders the other.”

Furthermore, this method is only applicable to polynomial expressions. If the original expression were exponential, the resulting difference rows would lead to recursive patterns.

Final Thoughts

We began by exploring straight lines and triangles, then ventured into the realm of finite differences. Despite its limitations, this method is valuable in studying real-world phenomena, numerical algorithms, and iterative mathematical schemes.

Now that you've been introduced to this method, how might you apply it in your own explorations?

References and Acknowledgments: Martin Gardner.

If you appreciate my work, consider showing your support by clapping, following, and subscribing. For further reading, you may find interest in "How To Really Solve This Combinatorics Puzzle" and "How To Approach the Straight Lines and Triangles Puzzle."