Chapter 1: Engaging Questions from Students

In this article, we continue our exploration of the intriguing inquiries made by my students, focusing on a timeless math challenge that involves a straightforward trick for its resolution. If you're curious, you can revisit the initial question in this series and the inspiration behind it by clicking here.

The first question raised by my students was one I had encountered before, albeit in a more challenging form. They asked:

Find all positive integers x and y, where x < y, that satisfy the equation:

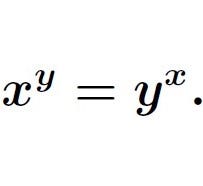
I encourage you to attempt this problem on your own before proceeding, as I reveal the answer below.

Initially, my students were quite impressed when I quickly identified that the only solutions were the pairs (x,y)=(2,4) and (x,y)=(4,2). However, their enthusiasm waned when I admitted that I had encountered this question long ago and simply recalled the solution.

I then challenged them to tackle the problem as I had first seen it:

Find all real values of x and y, where x < y, that satisfy the equation:

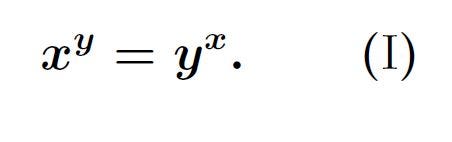
While some students proposed immediate solutions, they soon realized, after my hint, that there are infinitely many solutions. To their credit, by the following Monday, several students returned with correct answers.

Since first encountering this problem, I have learned various methods to solve it, many of which were introduced to me by my students. However, my preferred method remains the original one I was taught.

To begin, we note that with one equation and two unknowns, finding all solutions directly is impossible without clever guesses. Thus, we will make a substitution to facilitate our calculations. Specifically, I will express one variable, choosing y for this example, in terms of the other variable:

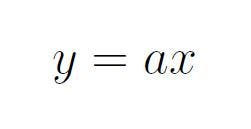
Here, a represents a real constant that satisfies the equation.

With this substitution, our original equation transforms into:

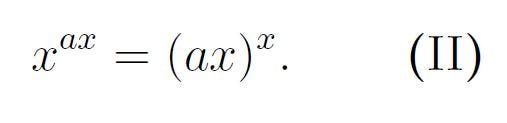
Next, we will apply the rules of indices. Recall that for any real numbers a, b, and c:

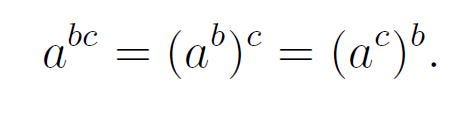
Thus, we can rewrite the transformed equation as:

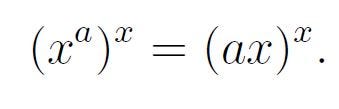
Since both sides now share the same exponent, we can conclude that:

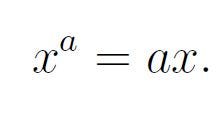
Next, we isolate x:

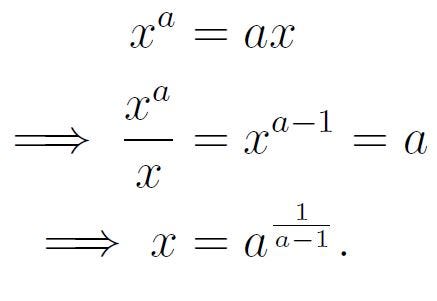
With x now determined, we substitute back to find y:

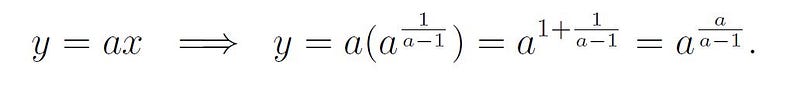
Thus, we conclude that the solution is:

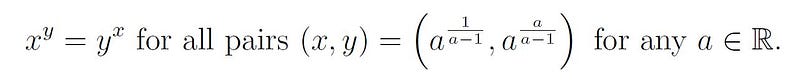
As a specific case, if we set a=2, we discover that (x,y)=(2,4) is indeed a valid solution. I challenge you to demonstrate that this is the only integer solution. I welcome your thoughts!

Thank you for reading. If you enjoy my work, consider following me and my publication, Y(Math), to help share these articles with a broader audience.

Chapter 2: Engaging Video Resources

This video titled "Can you solve this 4th grade problem?" presents a fun and engaging way to tackle elementary math challenges, perfect for sparking interest in young learners.

In this video titled "Can you solve an elementary school question from Singapore?" viewers will explore a unique problem-solving approach that can broaden their understanding of mathematics.