Chapter 1: An Introduction to Number Theory

What exactly are numbers? Are they merely constructs we've created? Why do we limit ourselves to the digits 0 to 9 instead of utilizing a broader range? Furthermore, why do we incorporate fractions and decimals alongside whole numbers? This branch of mathematics, which ponders over the nature and structure of numbers, is referred to as number theory.

The origins of number theory trace back to ancient civilizations, where mathematicians examined various numbering systems. This exploration provides insight into why we have accepted these systems in their current forms. Below are some notable number systems:

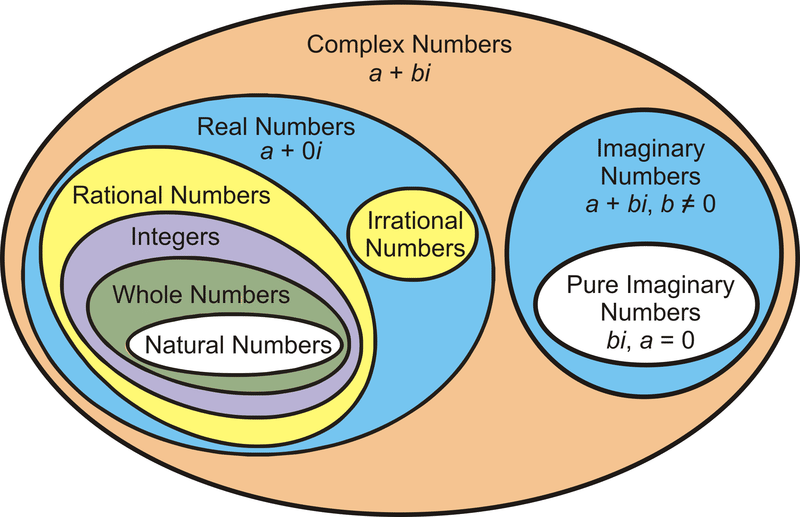
Natural Numbers: This category includes the positive integers—1, 2, 3, 4, 5, and so forth. These were the first known number system, as evidenced by early humans marking tallies on bones and cave walls to keep track of quantities.

Whole Numbers: Building upon natural numbers, the inclusion of "0" gave rise to whole numbers. The Babylonians contributed significantly by developing a place-holding notation for empty columns in numbers exceeding 9, such as "10," "1,000," and "1,090," where zeros signify absence in those places.

Integers: Integers expand upon the natural numbers by incorporating both positive and negative values along with zero. While we may take them for granted today, ancient mathematicians were skeptical of negative numbers. For example, subtracting 5 from 3 yields –2, which is particularly useful in financial contexts to denote losses. The Indian mathematician Brahmagupta, in 628 AD, illustrated the necessity of negative numbers for the advancement of arithmetic, leading to their acceptance.

Rational Numbers: Any number that can be articulated as a fraction (e.g., 2/3) falls under this category. This includes finite decimals and integers, as they can also be represented as fractions, such as 687/100 = 6.87 and 2/1 = 2. The term "rational" derives from the concept of ratios. Rational numbers became essential as various quantities, such as time and resources, couldn’t always be expressed in whole units. For instance, one may have to measure milk in parts of a gallon, or record running distances in fractions rather than whole miles.

Irrational Numbers: These numbers cannot be expressed as fractions. Notable examples include the square root of 2 and Euler’s number, e (approximately 3.14159…). There is a captivating history regarding irrational numbers. The Greek mathematician Pythagoras, who staunchly believed in the rationality of all numbers, even established a cult around the number 10, considering it divine. However, a follower named Hippasus demonstrated the square root of 2, challenging Pythagorean beliefs, which allegedly led to his demise.

Real Numbers: This category encompasses both rational and irrational numbers. In practical applications, especially in data science, any decimal can be treated as a real number.

Complex and Imaginary Numbers: These types arise when calculating the square root of negative numbers. Although they hold significance in specific problems, our focus will primarily remain on other number types.

Chapter 2: Understanding Number Theory Through Video Resources

To further explore number theory, consider watching the following educational videos:

The first video, "Number Theory for Beginners - Full Course," provides a comprehensive introduction to the subject, ideal for those new to the topic.

The second video, "The Foundation -- Number Theory 1," delves into the essential concepts that form the basis of number theory, paving the way for deeper understanding.

Thank you for engaging with the In Plain English community! We appreciate your participation.

Be sure to clap and follow the author!

Follow us on: X | LinkedIn | YouTube | Discord | Newsletter

Explore our other platforms: Stackademic | CoFeed | Venture | Cubed

Discover more content at PlainEnglish.io